آشنایی با آنالیز واریانس (ANOVA) برای تحلیل نتایج مقایسات بین آزمایشگاهی
1- مقدمه بر تحلیل نتایج مقایسات بین آزمایشگاهی
مطابق با الزامات استانداردهای ISO 15189:2022 و ISO/IEC 17025:2017 آزمایشگاه باید در جایی که مقتضی است و دسترسی وجود دارد، عملکرد خود را در مقایسه با نتایج سایر آزمایشگاهها پایش کند. این پایش باید طرحریزی و بازنگری شده و باید شامل یک یا هر دو روش زیر باشد، اما محدود به آنها نمیشود:
- شرکت در آزمون مهارت؛
- شرکت در مقایسات بین آزمایشگاهی به غیر از آزمون مهارت؛
دادههای به دست آمده در فعالیتهای کنترل کیفی داخلی و خارچی آزمایشگاه باید به نحوی ثبت شوند که روند آنها قابل تشخیص بوده و در جایی که قابل اجرا باشد، باید فنون آماری در بازنگری نتایج به کار گرفته شود. در بسیاری از مراکز آزمایشگاهی از آزمون های فرض آماری برای کنترل کیفیت نتایج آزمون و یا صحه گذاری روش های آزمون به منظور برآوزدهسازی الزامات استانداردهای ایزو ۱۷۰۲۵ و ایزو ۱۵۱۸۹ برای تحلیل نتایج استفاده میشود. در تجزیه و تحلیل مقایسات بین آزمایشگاهی و مطالعات درون آزمایشگاهی هنگامی که میخواهیم نتایج بیش از سه گروه مختلف (سه آزمایشگاه متفاوت و یا سه کارشناس متفاوت در یک آزمایشگاه، سه روش آزمون متفاوت و …) را به یکدیگر مقایسه کنیم، از روش آنالیز واریانس (ANOVA) استفاده میشود. روش ANOVA از F-test برای آزمون آماری برابری میانگینها استفاده میکند. در این پست، با استفاده از یک مثال عددی نحوه استفاده از آنالیز واریانس یک طرفه برای تچزیه و تحلیل نتایج مقایسات بین آزمایشگاهی با استفاده از نرم افزار minitab نشان داده خواهد شد که چگونه ANOVA و F-test را میتوان برای انجام مقایسات مورد استفاده قرارداد.
اما یک دقیقه صبر کنید … آیا تا کنون توجه کردهاید که چرا میخواهید از یک آنالیز واریانس برای تعیین اینکه آیا میانگینها متفاوت هستند، استفاده کنید؟
در این پست همچنین نشان داده خواهد شد که چگونه واریانس اطلاعاتی را در مورد میانگینها فراهم میکند. همانطور که در پست آشنایی با t-tests بجای معادلهها بر روی مفهوم و نمودارها تمرکز شد در این پست نیز بر روی مفهوم آنالیز واریانس تمرکز میشود.
2- آماره F و آزمون F چیست؟
F-tests و آماره آزمون آن، “F-statistic”، به افتخار رونالد فیشر نامگذاری شد. آماره F نسبت دو واریانس است. واریانس یک شاخص برای اندازهگیری میزان پراکندگی است، که نشان میدهد تا چه اندازه دادهها از میانگین پراکنده شده است. مقادیر بزرگتر واریانس نشان دهنده پراکندگی بیشتر است.
واریانس مربع انحراف استاندارد است. در بسیاری از علوم، استفاده از انحراف استاندارد بجایی واریانس رایجتر است، چرا که انحراف استاندارد هم واحد با دادههای اندازهگیری شده است ولی واریانس پرداکندگی را برحسب مربع واحد دادههای اندازه گیری شده، نشان میدهد. با این حال در بسیار از تجزیه و تحلیلهای واقعی از واریانس برای انجام محاسبات استفاده میکنند.
آماره F بر اساس به نسبت میانگین مربعات است. اصطلاح “میانگین مربعات” ممکن است گیج کننده باشد اما “میانگین مربعات”به سادگی برآورد واریانس جمعیت است که در آن درجات آزادی (DF) برای محاسبه و برآورد مورد استفاده قرار گرفته است. با این حال، با تغییر واریانس که شامل نسبت است، آزمون F یک آزمون بسیار انعطاف پذیر میشود.
3- استفاده از آزمون F در آنالیز واریانس یک طرفه
برای استفاده از آزمون F برای تعیین اینکه آیا میانگینها گروهها مختلف با هم برابر هستند، در آنالیز واریانس یک طرفه، از آماره F به صورت زیر استفاده میشود:
بهترین راه برای درک نسبت فوق در آزمون واریانس یک طرفه استفاده از یک مثال برای تشریح آن است.
مثال: استحکام کششی یک نمونه پلاستیکی توسط چهار آزمایشگاه مختلف مورد آزمون قرار گرفته است. دادههای مربوط به این مثال از لینک (دانلود مثال استحکام کششی) قابل دانلود است. برای مشاهده و تجزیه و تحلیل داده های مربوط به این مثال لازم است نرم افزار minitab را بر روی سیستم خود نصب کنید.
آخرین ویرایش نرم افزار MINITAB میتوانید در بخش نرمافزارهای کاربردی سایت دانلود نمایید.
برای توضیح مفاهیم مربوط به آنالیز واریانس ما از خروجی این نرم افزار استفاده میکنیم. پس از نصب نرم افزار و دانلود مثال، برای تجزیه و تحلیل نتایج در نرم افزار MINITAB مسیر زیر را دنبال کنید:
Stat > ANOVA > One-Way ANOVA…
In the dialog box, choose “Strength” as the response, and “Sample” as the factor
Press Ok
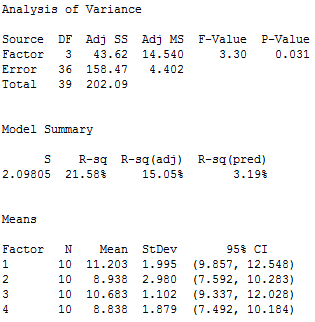
نرم افزار MINITAB در پنجره Session خروجی زیر را نشان میدهد:
صورت کسر: تغیرپذیری بین میانگین آزمایشگاهها
آنالیز واریانس یک طرفه میانگین نتایج آزمون هر یک از چهار آزمایشگاه را به صورت مجزا محاسبه میشود. در مثال ارائه شده میاگین نتایج هر کدام از آزمایشگاهها به ترتیب عبارتند از: ۱۱٫۲۰۳, ۸٫۹۳۸, ۱۰٫۶۸۳ و ۸٫۸۳۸٫
این میانگینهای آزمایشگاهها در اطراف میانگین کل برای همه ۴۰ مشاهدات که برابر با ۹٫۹۱۵ میباشد، توزیع شده است. اگر میانگینهای نتایج آزمایشگاهها نزدیک به میانگین کل باشند، واریانس آنها کم است و اگر میانگینها آزمایشگاهها فاصله بیشتری از میانگین کل داشته باشد، واریانس آنها بیشتر است.
واضح است که اگر قرار است که نشان داده شود که میانگینها آزمایشگاهها یکسان هستند، در صورتی که میانگینها به یکدیگر نزدیکتر باشند، به این امر کمک خواهند کرد. در این شرایط تغیرپذیری کمتر بین میانگینها نتایج آزمایشگاه ها مطلوب خواهد بود.
تصور کنید که دو آنالیز واریانس یک طرفه مختلف که در آن هر آنالیز چهار گروه دارد، انجام شده است. نمودار زیر پراکندگی میانگینها را نشان می دهد. هر نقطه نشاندهنده میانگین نتایج یک گروه است. پراکندگی بیشتر در میانگین نتایج هر گروه، سبب پراکندگی بیشتر در صورت کسر آماره F میشود.

چه مقدار برای اندازه گیری واریانس بین آزمایشگاهها برای مثال استحکام کششی یک نمونه پلاستیکی بدست میآید؟
در خروجی آنالیز واریانس یک طرفه، (ADJ MS) برای Factor که مقدار آن برابر با ۱۴٫۵۴۰ برای اندازه گیری واریانس بین آزمایشگاهها استفاده میشود. هیچ گاه سعی نشود برای این مقدار تفسیری را بیان گردد، این عدد (۱۴٫۵۴۰) مجموع مجذور انحرافات تقسیم بر درجه آزادی فاکتورها میباشد. فقط در نظر داشته باشید که هر چه میانگین نتایج آزمایشگاه ها بیشتر از هم دوره باشند، این مقدار بزرگتر است.
مخرج کسر: تغییرپذیری درون آزمایشگاهی
پس تخمین صورت کسر آماره F، نیاز به یک تخمین از تغییرپذیری در هر آزمایشگاه برای تعیین مخرج آماره F وجود دارد. برای محاسبه این تخمین (واریانس)، نیاز به محاسبه اینکه هر مشاهد از میانگین نتایج آزمایشگاه خود چقدر فاصله دارد برای کل ۴۰ مشاهده وجود دارذ. به طور فنی، مقدار آن برابر با مجموع مجذور انحراف از هر مشاهده از میانگین نتایج آن آزمایشگاه تقسیم بر خطا درجه آزادی (DF) است.
اگر مشاهدات هر یک از آزمایشگاه نزدیک به میانگین نتایج آزمایشگاه خود هستند، واریانس درون آزمایشگاهی کم است. با این حال، اگر مشاهدات برای هر آزمایشگاه از مقدار میانگین برای آن آزمایشگاه فاصله زیادی داشته باشد، واریانس درون آزمایشگاهی مقدار بزرگی خواهد شد.

در نمودار فوق گراف سمت چپ تغییرپذیری کم درون آزمایشگاهی را نشان میدهد و گراف سمت راست تغییرپذیری زیاد درون آزمایشگاهی را نشان میدهد تغییرپذیری زیاد درون آزمایشگاهی سبب بزرگ شدن مخرج کسر در آماره F میشود. اگر علاقه مند به نشان دادن یکسان بودن میانگینهای بدست آمده در آزمایشگاههای مختلف باشیم، زمانی که واریانس درون آزمایشگاهی زیاد است، برای ما مطلوب خواهد بود.
برای این مثال آنالیز واریانس یک طرفه، تغییرپذیری درون آزمایشگاهی Adj MS برای Error خواهد بود که مقدار عددی آن برابر با ۴٫۴۰۲ است. آن در نظر گرفته شده به عنوان “Error” چون این تغییرپذیری ناشی از فاکتورها (آزمایشگاهها) نیست.
4- آماره F : تغییرپذیری بین آزمایشگاهی تقسیم بر تغییرپذیری درون آزمایشگاهی
از آماره F به عنوان آماره آزمون برای F-tests است. به طور کلی، آماره F نسبت دو مقدار تشریح شده در صورت و مخرج کسر است. در ادامه برای انجام تجزیه و تحلیل میتوان آزمونهای فرض زیر را تعریف کرد:
فرض ۰: میانگین نتایج آزمایشگاهها تفاوت معنادار آماری با یکدیگر ندارد.
فرض ۱: میانگین نتایج آزمایشگاهها تفاوت معنادار آماری با یکدیگر دارد.
که در آزمون فوق برای فرض صفر انتظار میرود این مقدار برای نسبت تغییرپذیری بین آزمایشگاهی تقسیم بر تغییرپذیری درون آزمایشگاهی برابر “۱” باشد و برای فرض یک انتظار میرود این مقدار نسبت مخالف “۱” باشد.
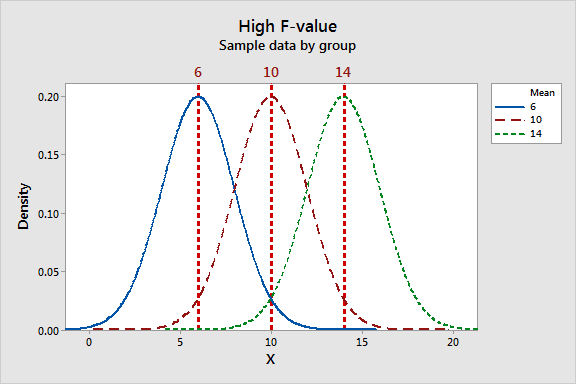
آماره F ترکیبی از نسبت تغییرپذیری بین آزمایشگاهی و درون آزمایشگاهی است. باید بررسی شود که تغییرپذیری بین آزمایشگاهی و درون آزمایشگاهی چگونه بر روی مقدار آماره F تاثیر میگذارد. به نمودار زیر نگاه کنید و پهنای پراکندگی میانگین آزمایشگاهها را با پهنای پراکندگی نتایج درون هر آزمایشگاه مقایسه کنید.
 | 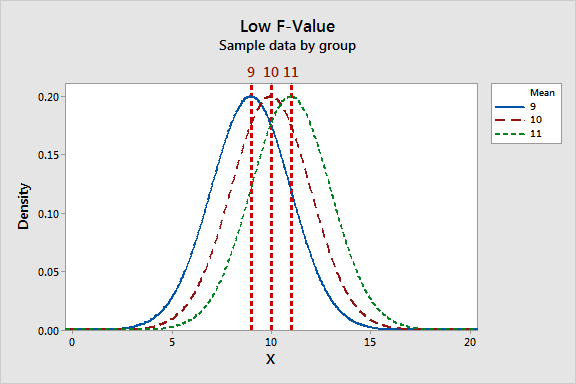 |
در نمودار سمت چپ که در آن برای آماره F مقدار پایین بدست آمده است، میانگین نتایج آزمایشگاهها نزدیک به هم هستند یعنی آنکه تغییرپذیری بین آزمایشگاهی نسبت به تغییر پذیری درون آزمایشگاهی عدد کوچکی میشود.
در نمودار سمت راست که در آن برای آماره F مقدار بزرگی بدست آمده است، میانگین نتایج آزمایشگاهها با هم فاصله زیادی دارند یعنی آنکه تغییرپذیری بین آزمایشگاهی نسبت به تغییر پذیری درون آزمایشگاهی عدد بزرگی شده است. برای پذیرش یا عدم پذیرش فرض صفر (یکسان بودن میانگین نتایج آزمایشگاهها) نیاز به مقدار بحرانی برای آماره F وجود دارد.
در این مثال برای تجزیه و تحلیل نتایج مقایسات بین آزمایشگاهی تغییر پذیری بین آزمایشگاهی (Factor Adj MS) برای صورت کسر برابر با ۱۴٫۵۴۰ و تغییر پذیری درون آزمایشگاهی (Error Adj MS) برای مخرج کسر برابر با ۴٫۴۰۲ شده است، که مقدار F برابر با ۳٫۳۰ را می دهد.
اینک سئوالی که پیش میآید آن است که “آیا مقدار F ما به اندازه بزرگ است که نتیجه گیری شود نتایج آزمایشگاههای مختلف، تفاوت معنادار آماری دارند؟” برای پاسخگویی به این پرسش میتوان از جداول آماری یا از محاسبه احتمالات توزیع F میتوان استفاده نمود.
5- توزیع F و آزمون فرض آماری
برای آنالیز واریانس یک طرفه، نسبت تغییرپذیری بین آزمایشگاهی و تغییرپذیری درون آزمایشگاهی همگامی فرض صفر درست است از تابع توزیع F پیروی می کند.
هنگامی که انجام آنالیز واریانس یک طرفه برای مطالعه، یک مقدار F به دست میآید. با این حال، اگر ما چندین نمونه های تصادفی با سایز یکسان از جمعیت یکسان برداشته شود آنالیز واریانس یک طرفه ANOVA انجام شود، مقادیر متفاوتی از F بدست میآید و میتوان توزیع همه آنها را رسم نمود. این نوع از توزیع به عنوان یک توزیع نمونه شناخته شده است.
از آنجا که در توزیع F فرض میشود که فرضیه صفر درست است، میتوان احتمال درست بودن فرض صفر را از تابع توزیع F محاسبه نمود. اگر احتمال درست بودن فرض صفر کم باشد، می توان نتیجه گیری نمود که شواهدی کافی برای رد فرض صفر وجود دارد. احتمال درستی فرض صفر را بنام p-value میشناسند.
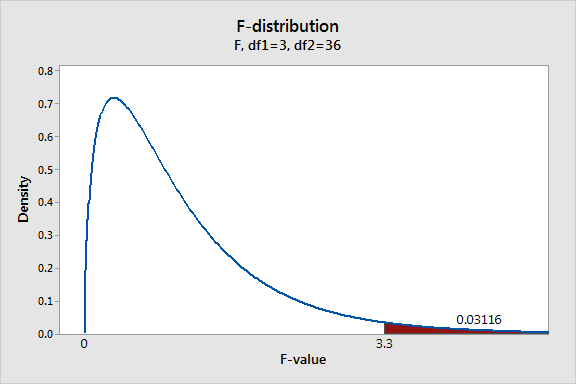
اگر فرضیه صفر درست باشد و ما مطالعه خودمان را چندین بار تکرار کنیم نمودار فوق برای توزیع مقادیر F بدست خواهد آمد. ناحیه قرمز رنگ احتمال مشاهده یک مقدار برای F که بزرگتر از F بدست آمده برای مثال (۳٫۳) را نشان میدهد. مقدار احتمال بدست آمده برای F در ناحیه قرمز رنگ ۳٫۱% است. این مقدار به اندازه کافی کوچک است که بتوان فرض صفر را در سطح معناداری ۰٫۰۵ (سطح اطمینان ۹۵%) رد کرد. لذا میتوان نتیجه گرفت که میانگین نتایج آزمایشگاههای مختلف با هم یکسان نیست و از نظر آماری تفاوت معناداری دارند.
6- بررسی میانگینها به وسیله آنالیز تغییرپذیری
آنالیز واریانس ANOVA از آزمون F برای تعیین اینکه آیا تغییرپذیری بین آزمایشگاهی بزرگتر از تغییرپذیری درون آزمایشگاهی است، استفاده میکند. در صورتی که این نسبت به اندازه کافی بزرگ باشد، میتوان نتیجه گیری کرد که میانگین نتایج همه آزمایشگاهها با هم یکسان نیستند.
7- سخن پایانی
امیداوریم نحوه استفاده از روش آنالیز واریانس ANOVA را برای تحلیل نتایج مقایسات بین آزمایشگاهی و همچنین برآورده سازی الزامات استاندارد استاندارد ایزو 17025 و ایزو 15189 برای استفاده از فنون آماری برای تجزیه و تحلیل نتایج را به خوبی فراگرفته و از این مطلب لذت برده باشید. در صورت وجود هر گونه پرسشی در خصوص انجام مقایسات بین آزمایشگاهی یا تجزیه و تحلیل نتایج بدست آمده در مقایسات بین آزمایشگاهی میتواند سوالات خودتان در قسمت کامنت های این پست قراردهید. سعی خواهد شد تا جای ممکن به سئوالات مطرح شده پاسخ مناسب داده شود. همچنین در صورت نیاز به برگزاری دوره آموزشی آشنایی با روشهای آماری در مقایسات بین آزمایشگاهی و آزمون مهارت برای کارکنان آزمایشگاه یا برای دریافت خدمات مشاوره برای اخذ گواهینامه ایزو 17025 و مشاوره ایزو 15189 میتوانید با ما تماس بگیرید.
19 دیدگاه
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.


خبلی عالی است لطفا بیشتر مثال بزنید
من مثاله واسم نیومد
بسیار عالی بود جناب دکتر
خیلی از سوالاتم جواب داده شد و البته خیلی سوالات جدیدی نیز برام ایجاد شد!
ممنون از مطالب جالبی که گذاشتید
سلام و سپاس
برای انجام این آزمون در متغیر وابسته باید جمع سوالات پرسشنامه رو بگذاریم یا میانگین سوالات را؟
با سلام و احترام
متغیرهای مستقل شما چیست؟
سلام من یه سوال داشتم ممنون میشم راهنماییم کنید من درجدول انالیز واریانس داده های پایان نامم df در lack of fit مساوی یک شده داور ایراد گرفته و دور اون رو خط کشیده من نمیدونم چه مشکلی داره ؟فیلم های زیادی هم نگاه کردم ولی بیشتر در مورد p -valueو Rها توضیح دادن
سلام
ممنون بابت مطالب عالیتون
آیا راجع به دو روش tan θ test و welch test که مربوط به مقایسه دو میانگین با واریانس های متفاوت میباشد اطلاعاتی دارید؟
با تشکر
با سلام و احترام
به چه اطلاعاتی نیاز دارین؟
میشه راجب tan θ test توضیح بدین که به چه صورت هست؟من شدیدا بهش احتیاج دارم و هیچجا ننوشته
منم دقیقا دنبال همین موضوع هستم اگه کسی میدونه کمک کنه ممنون میشم
سلام من یه سوال داشتم ممنون میشم راهنماییم کنید من درجدول انالیز واریانس داده های پایان نامم df در lack of fit مساوی یک شده داور ایراد گرفته و دور اون رو خط کشیده من نمیدونم چه مشکلی داره ؟فیلم های زیادی هم نگاه کردم ولی بیشتر در مورد p -valueو Rها توضیح دادن0
درجه آزادی در آمار (Degree of Freedom) بیانگر تعداد مقادیری است که در یک محاسبه مرتبط با شاخص یا برآوردگرهای آماری، میتوانند آزادانه تغییر کنند. این مفهوم در بسیاری از موضوعات و حوزههای علم آمار مورد استفاده قرار میگیرد.
در نظریهٔ برآورد:
تعداد مقادیری که یک آماره امکان تغییر دارد
تعداد مشاهدات مستقل منهای تعداد پارامترهای برآورد شده.
بهطور معادل: تعداد مشاهدات مستقل منهای تعداد روابط معلوم میان مشاهدات
در نظریه آزمون:
بعد فضای مجهول (مدل کامل) منهای بعد فضای مفروض (مدل مقید)
احتمالا منظور داور این بوده که تعداد مشاهدات بیشتری را بکار بگیرین که درجه آزادی شما بزرگتر شود تا به توان آزمون بزرگتری دست یابید.
ممنون از راهنمایتون
منم دقیقا دنبال همین موضوع هستم اگه کسی میدونه کمک کنه ممنون میشم
سلام. سپاس از مطلب بسیار مفیدتون. در متن یک لینگ گذاشتید در رابطه با t-test ولی درست کار نمیکنه. لطفا این لینک را درست کنید.
با سلام و احترام
سپاسگزارم از اطلاع رسانی شما
لینک اصلاح گردید.
موفق باشید
دستمردی
سلام.واقعا وبسایت خوبی دارید
سلام.خواستم بابت وبسایت خوبتون ازتون
تشکر کنم و امیدوارم باعث ایجاد انگیزه براتون
بشه
با سلام و عرض ادب. در تجزیه واریانس داده ها مقدار f بی نهایت شده است. از sas برای تجزیه استفاده کرده ام. طرح آزمایش هم طرح آشیانه ای بوده است. بی زحمت اعلام نطر فرمایید که چرا این اتفاق افتاده و ایا مشکلی ندارد؟؟؟