معرفی آنالیز پایداری فون نویمان برای کشف وجود رانش در اندازه گیری
1- مقدمه
در تجزیه و تحلیل سیستمهای اندازهگیری، تحلیل پایداری فون نویمان (که به عنوان آنالیز پایداری فوریه نیز شناخته میشود) یک فرایند برای بررسی پایداری نتایج اندازهگیری (رانش در اندازه گیری) است که به معادله دیفرانسیل با مشتقات پارهای اعمال میشود. اساس این آنالیز تجزیه سری فوریه خطاهای عددی است و پس از مقاله کوتاهی در سال ۱۹۴۷ توسط محققان انگلیسی، کرنک و نیکلسون، در آزمایشگاه ملی لس آلاموس توسعه یافت. این روش یک نمونه از انتگرالگیری زمانی صریح است که تابع توصیفکننده معادله حاکم در زمان جاری مقداردهی میگردد. بعدها، این روش به شکلی دقیقتر از سوی جان فون نویمان در مقاله دیگری ارائه شد. در این پست قصد داریم با استفاده از آنالیز پایداری فون-نویمان نحوه شناسایی وجود رانش دستگاهی (Instrumental drift) در نتایج بدست آمده از تجهیزات اندازهگیری تشریح نمایم. رانش دستگاهی (Instrumental drift) در واژه نامه اندازه شناسی (VIM) به صورت زیر تعریف شده است:
“تغییرات مداوم یا تدریجی نشاندهی در طول زمان، به علت تغییرات خصیصههای اندازهشناختی یک وسیله اندازه گیری است.”
2- آنالیز پایداری فون نویمان برای کشف رانش در اندازه گیری
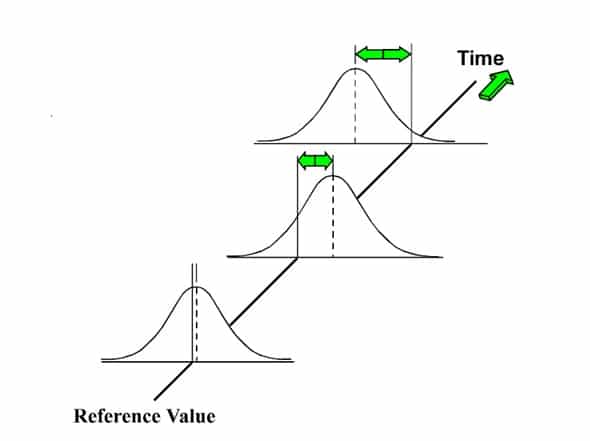
پایداری نتایج اندازهگیری همراهی نزدیکی با خطای نتایج دارد. نتایج اندازهگیری زمانی پایدار است که خطاهای تولیدی در محاسبه یک گام زمانی باعث بزرگنمایی خطاها در ادامهی محاسبه نشود. یک نتیجه آزمون که به صورت ذاتی پایدار میباشد، نتیجهای است که خطاها آن در طول زمان ثابت بمانند. به عبارت دیگر اگر خطاها کاهش بیابند و در آخر از بین بروند، نتایج اندازهگیری پایدار خوانده میشود. در غیر این صورت اگر خطاها با گذر زمان رشد کنند نتایج اندازهگیری را ناپایدار میخوانند. پایداری نتایج اندازهگیری به وسیله ی آنالیز پایداری فون نیومن میتواند مورد بررسی قرارگیرد.
برای بررسی پایداری نتایج فرض کنید نتیجه n اندازهگیری متوالی X1, X2, … , Xn بر روی یک استاندارد در فواصل زمانی مشخص بدست آمده است و میخواهیم وجود رانش (Drift) در نتایج اندازهگیری را بررسی نمایم. “رانش داشتن” (drifting) حالتی است که نتایج به صورت پیوسته به طرف بالا (یا به طرف پایین) حرکت میکنند. آماره مورد استفاده برای کشف چنین رانشی (که ابتدا در سال 1941 توسط فون نیومان برای کشف رانش در دادههای سری زمانی معرفی گردید) عبارت است از:
میتوان نشان داد که آماره M برای هر مجموعه دادهها باید بین 0 تا 4 باشد. مقادیر M نزدیک به 2 بیانگر تصادفی بودن دادهها (فقدان رانش) میباشد، در حالیکه مقادیر M نزدیک به 0 نشاندهند وجود رانش در دادهها است. مقادیر M نزدیک به 4 در موارد بسیار نادری که دادهها بسرعت در اطراف مقدار میانگین بالا و پایین میروند اتفاق میافتد. این حالت اخیر در کاربردهای سیستم اندازهگیری نادر میباشد و به بررسی آن در اینجا نمیپردازیم.
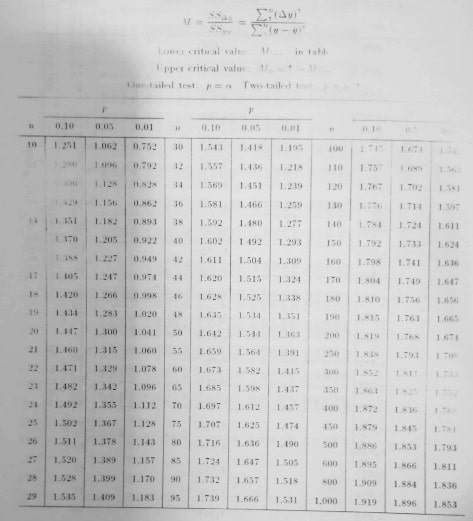
برای تعیین اینکه رانش قابل توجهای در اندازهها وجود ندارد (M نزدیک به 2 میباشد) یا رانش قابل توجه وجود دارد (M نزدیک 0 است) مراجعه به جدول زیر لازم است. در یک سطح اهمیت α، هر گاه M کمتر از M1- α مشخص شده در جدول باشد، رانش از لحاظ آمای معنادار اعلام میشود. در غیر این صورت، نتیجهگیری میشود که رانش معناداری وجود ندارد.
3- مثال: برای کشف رانش در اندازه گیری تجهیزات
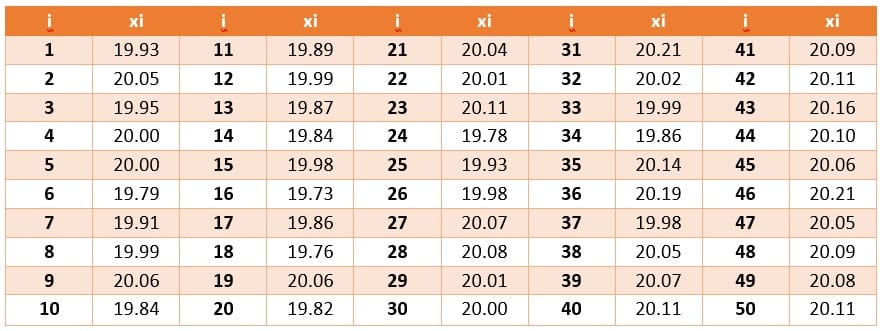
نتایج مربوط به آزمون بر روی یک نمونه با مقدار مرجع گواهی شده 20 در 50 روز متوالی مطابق با جدول زیر است.
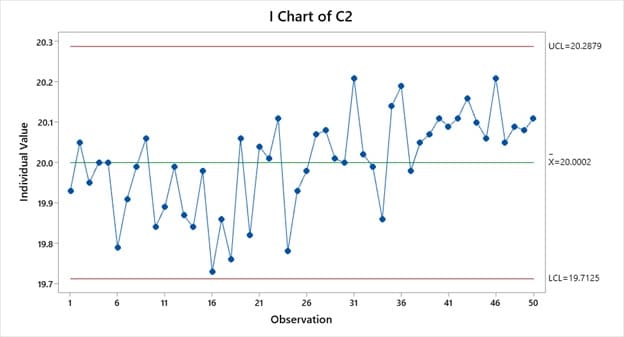
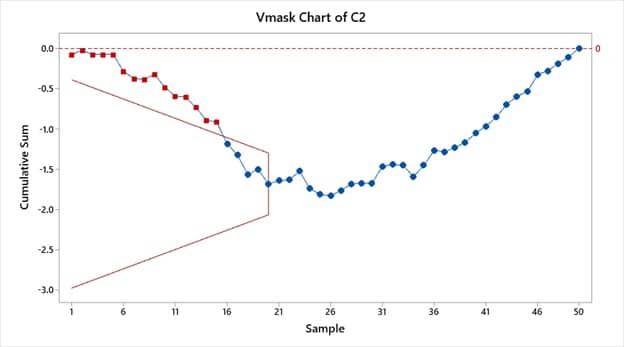
برای دادههای جدول فوق نمودار مشاهدات انفرادی و نمودار کیوسام با استفاده از نرم افزار Minitab 19 رسم شده است.
برای دادههای ارائه شده در مثال فوق M عبارت است از:
با توجه به آنکه مقدار M بدست آمده (1.353) از مقدار بحرانی M1- α کمتر است، نتیجه میگیریم (در سطح اهمیت α=0.05) برای نتایج اندازهگیریهای ارائه شده در مثال فوق مقداری رانش معنادار وجود دارد. این نتیجه با آنچه از بررسی چشمی نمودارهای کنترل این دادهها بدست آمده همخوانی دارد.
وقتی بر اساس آماره M از آزمون رانش استفاده میکنیم، به یک نکته باید توجه داشته باشیم، این آزمون تنها به رانش دادهها حساس است، و قادر به کشف اریبیهای سیستماتیک (Systematics Biases) در اندازهگیریها نمیباشد. برای دیدن این نکته، فرض کنید که دادههای X1, X2, … , Xn همگی به یک اندازه ثابت C تغییر پیدا کرده باشند. برای دادههای جدید X1+C, X2+C, … , Xn+C عبارت صورت معادله M بدون تغییر باقی میمانند زیرا Xi+C) – (Xi-1 +C) = Xi-Xi-1). به روشی مشابه میتوان دید که عبارت مخرج نیز بدون تغییر باقی خواهد ماند. بدین ترتیب افزایش همه دادهها به یک اندازه ثابت C اثر بر روی مقدار M ندارد.
نحوه محاسبه عدمقطعیت ناشی از رانش ابزار اندازهگیری
4- برگزاری دورههای آموزشی تخمین عدم قطعیت با نرم افزار QMSys GUM
جهت هماهنگی برای برگزاری دوره “برآورد عدم قطعیت اندازه گیری با نرم افزار QMSys GUM” میتوانید با ما تماس بگیرید.


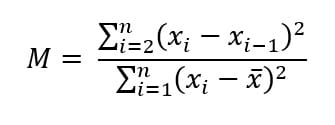
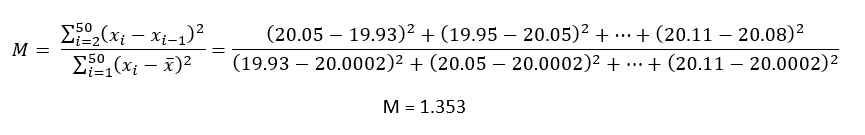
دیدگاهتان را بنویسید