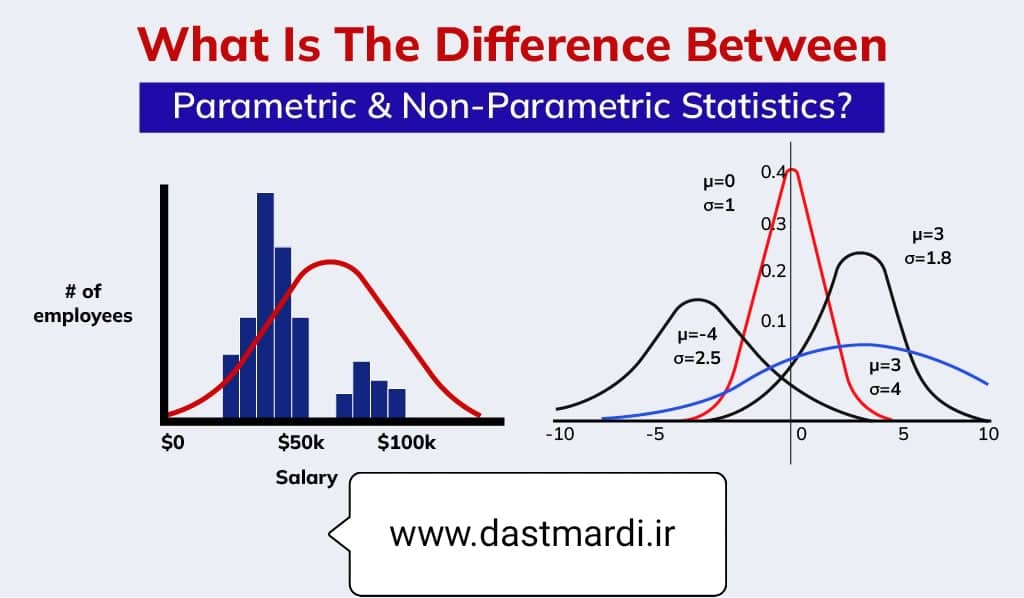
۱- مقدمه بر آزمون پارامتریک و ناپارامتریک

در این پست آموزشی در نظر داریم نحوه انتخاب بین آزمون پارامتریک و ناپارامتریک در مقایسات درون آزمایشگاهی و مقایسات بین آزمایشگاهی را تشریح نماییم. اکثر کارکنان مراکز آزمایشگاهی که از تجزیه و تحلیل آماری برای مقایسات درون و بین آزمایشگاهی استفاده می‌کنند با تجزیه و تحلیل پارامتریک (مانند آزمون‌های T-test, F-test, ANOVA) بیشتر از تجزیه و تحلیل ناپارامتریک (مانند آزمون‌های sample Sign, sample Wilcoxon, Mann-Whitney) آشنایی دارند. آزمون ناپارامتریک آزمون توزیع آزاد نامیده می شوند زیرا در آنها فرض این که داده‌ها از توزیع توزیع خاص پیروی می‌کنند، وجود ندارد. هرگاه داده‌ها از فرضیات آزمون‌های پارمتریک پیروی نکنند (مثل فرض نرمال بودن داده‌ها) باید از آزمون‌های ناپارامتریک استفاده نمود. به نظر می رسد بررسی نرمال بودن داده‌ها یک راه خوب و ساده برای انتخاب بین آزمون‌های پارامتریک و ناپارامتریک است، اما در این خصوص ملاحظاتی وجود دارد که باید مدنظر قرار گرفته شوند. در این پست، تشریح خواهد شد که چه زمانی باید از آزمون‌های زیر استفاده نمود:

– تجزیه و تحلیل پارامتریک برای آزمون گروه میانگین ها.

– تجزیه و تحلیل ناپارامترکی برای آزمون گروه میانه ها.

به طور خاص، بر روی یک دلیل مهم برای استفاده آزمون ناپارامتریک تمرکز می‌شود که به اندازه کافی به آن پرداخته نشده است!

---

۲- آزمون فرض برای میانگین و میانه

آزمون‌های ناپارامتریک مانند یک دنیای موازی با آزمون‌های پارامتریک هستند. جدول زیر آزمون‌های پارامتریک و ناپارامتریک معادل هم را در نرم افزار Minitab نشان می‌دهد.

آزمون پارامتریک (میانگین)	آزمون ناپارامتریک (میانه)
۱-sample t test	۱-sample Sign, 1-sample Wilcoxon
۲-sample t test	Mann-Whitney test
One-Way ANOVA	Kruskal-Wallis, Mood’s median test
Factorial DOE with one factor and one blocking variable	Friedman test

---

۳- دلایل استفاده از آزمون‌های پارامتریک در مقایسات درون آزمایشگاهی و مقایسات بین آزمایشگاهی

دلیل ۱: آزمون پارامتریک به خوبی می تواند برای توزیع غیر نرمال انجام شود.

این امر ممکن است تعجب آور باشد، اما آزمون پارامتریک می توانید به خوبی با داده‌های پیوسته که غیر نرمال هستند انجام شود. اگر اندازه نمونه‌ها مطابق با جدول زیر تامین شود.

پارامتریک آنالیز	اندازه نمونه برای داده‌های غیر نرمال
۱-sample t test	بیشتر از ۲۰
۲-sample t test	هر گروه باید بزرگتر از ۱۵ باشد.
One-Way ANOVA	اگر ۲ تا ۹ گروه داشته باشید، هر گروه باید بیشتر از ۱۵ نمونه باشد. اگر ۱۰ تا ۱۲گروه داشته باشید، هر گروه باید بیشتر از ۲۰ نمونه باشد.

دلیل ۲: آزمون پارامتریک را زمانی که پراکندگی در بین گروه‌های مورد مقایسه متفاوت است، می‌توان انجام داد.

در آزمون ناپارامتریک فرض پیروی داده‌ها از توزیع نرمال لازم نیست، اما فرضیات دیگری دارد که برآورده سازی آنها به مراتب سخت‌تر است. برای آزمون ناپارامتریک مقایسه چند گروه، فرض رایج این است که داده‌ها همه گروه باید پراکندگی یکسان داشته باشد. اگر گروه‌ها پراکندگی‌های مختلفی داشته باشند، آزمون ناپارامتریک ممکن است نتایج معتبر ارائه ندهد. از سوی دیگر، اگر شما در نرم افزار minitab  از آزمون ۲-sample t test یا آنالیز واریانس یک طرفه استفاده کنید، شما می توانید به سادگی به قسمت تنظیمات بروید و تیک گزینه فرض برابری واریانس را بردارید. این گزینه برای زمانی که پراکندگی داده‌ها در گروه‌های مختلف یکسان نیست، می‌تواند بسیار مفید باشد.

 دلیل ۳: توان آماری

آزمون پارامتری معمولاً توان آماری بیشتر از آزمون ناپارامتری دارد (خطای نوع دوم آنها کوچکتر است). بنابراین، تشخیص اثر معنی‌دار زمانی که یکی واقعا وجود دارد، با احتمال بیشتری اتفاق می‌افتد.

---

۴- دلایل استفاده از آزمون ناپارامتریک در مقایسات درون آزمایشگاهی و مقایسات بین آزمایشگاهی

دلیل ۱: میانه نتایج وضعیت ناحیه مورد مطالعه را بهتر نشان می‌دهد.

یکی از دلایل بسیار مهم  برای استفاده آزمون غیر پارامتریک این است که اندازه کافی از داده‌های مورد نیاز در دسترس نمی‌باشد. این واقعیت که می توان از آزمون پارامتری با داده های غیر نرمال استفاده نمود، بدان معنا نیست که میانگین بهترین عامل برای نشان دادن مرکزیت داده‌ها است. به عنوان مثال، مرکز توزیع نامتقارنی مانند درآمد، می توان با میانه نشان داده شود. میانه نقطه‌ای است که در آن ۵۰ درصد داده‌ها بزرگتر از آن و ۵۰ درصد کوچکتر از آن هستند، اگر شما چند میلیاردر به نمونه‌های مورد مطالعه اضافه نمایند، میانگین ریاضی تا حد زیادی افزایش می‌یابد حتی اگر درآمد برای افراد معمولی تغییر نکند. بنابراین هنگامی که توزیع داده ها به اندازه کافی متقارن نیست، میانگین به شدت تحت تاثیر تغییرات در نقاط انتهای توزیع قرار می‌گیرد در حالی که میانه کمتر تحت تاثیر مقادیر نقاط انتهای توزیع قرار می‌گیرد.

 دلیل ۲: وقتی تعداد نمونه‌ها بسیار کوچک است

اگر رهنمودهای اندازه نمونه برای آزمون پارامتری برآورده نشوند و اطمینان از این که داده‌ها دارای توزیع نرمال هستند، وجود نداشته باشد. باید از آزمون ناپارامتری استفاده شود. هنگامی که اندازه نمونه واقعا کوچک باشد، ممکن است حتی قادر به تعیین توزیع داده آن نباشیم. در این سناریو، آزمون ناپارامتری نتایج بهتری برای تجزیه و تحلیل و مقایسات درون و بین آزمایشگاهی را ارائه می‌دهد.

دلیل ۳: هنگامی که داده‌های ترتیبی، رتبه‌ای، و یا نقاط دورافتاده که نمی توان آنها را حذف کرد، وجود داشته باشد.

معمولا آزمون پارامتریک تنها می تواند داده‌های پیوسته را ارزیابی کند و نتایج ارزیابی می توان به طور قابل توجهی توسط نقاط دور افتاده تحت تاثیر قرار گیرد. در مقابل، برخی از آزمون ناپارامتری می تواند داده های ترتیبی، داده‌های رتبه‌ای را مورد ارزیابی قرار دهند، و به طور موثری تحت تاثیر داده های پرت قرار نمی گیرند.

برای بررسی فرضیات جهت آزمون ناپارامتری مطمئن شوید، زیرا هر یک از آنها الزامات داده خود را دارند.

---

۵- جمع بندی برای انتخاب بین آزمون پارامتریک و ناپارامتریک

این تصور معمولاً وجود دارد که نیاز به انتخاب بین آزمون پارامتریک و ناپارامتریک هنگامی رخ می‌دهد که داده‌های شما قادر به برآوردن فرضیه‌های آزمون‌های پارامتریک نباشد. این می‌تواند در مواردی که هم یک اندازه نمونه کوچک و داده غیر نرمال رخ دهد. با این حال، ملاحظات دیگر اغلب نقش بازی می‌کنند زیرا آزمون پارامتریک اغلب می‌تواند برای داده‌های غیرنرمال را نیز بکار روند. در مقابل، آزمون ناپارامتری مفروضات سختی دارند که نمی‌توانید نادیده گرفته شوند. تصمیم‌گیری اغلب به این بستگی دارد که میانگین یا میانه، کدامیک مرکز توزیع داده ها درست‌تر نشان می‌دهد.

• اگر میانگین به درستی نشان دهنده مرکز توزیع باشد و حجم نمونه به اندازه کافی بزرگ است آزمون‌های پارامتریک، را بخاطر قدرتمندی آنها استفاده نماید.
• اگر میانه مرکز توزیع را بهتر نشان می دهد، حتی زمانی که شما یک اندازه نمونه بزرگ دارید از آزمون‌های ناپارامتریک استفاده نماید.

در نهایت، اگر تعداد نمونه بسیار کوچک باشد، شما ممکن است در استفاده از آزمون ناپارامتریک دچار مشکل شوید. در این موارد نمونه‌های بیشتری را باید مورد بررسی قرار داد. زیرا هنگامی که یک اندازه نمونه کوچک دارید و نیاز به استفاده از آزمون ناپارامتریک با کارآمدی کمتر می باشد، شانس تشخیص اثر معنی‌دار زمانی که وجود دارد، می‌تواند بسیار کوچک باشد. 

سخن پایانی

در این پست آموزشی تفاوت بین روش‌های پارامتریک و ناپارامتریک برای انجام تجزیه و تحلیل‌های آماری نتایج مقایسات درون آزمایشگاهی و بین آزمایشگاه تشریح گردید و نکاتی که بایستی هنگام انتخاب روش آماری مناسب برای تحلیل فعالیت‌های کنترل کیفی داخلی و خارجی در نظر گرفته شود، ذکر گردید. در یک پست آموزشی با عنوان فلوچارت انتخاب آزمون آماری مناسب نحوه انتخاب بین سایر روش‌های آماری برای انجام تجزیه و تحلیل بر روی نتایج تشریح شده است. همچنین در صورت نیاز به برگزاری دوره آموزش آشنایی با روش‌های آماری در مقايسات بين آزمايشگاهی می‌توانید با ما تماس بگیرید.