کاربرد نمودارهای کنترل جمع تجمعی در آزمایشگاه

1- مقدمه بر نمودارهای کنترل جمع تجمعی

نمودارهای کنترلی یکی از ابزارهای مفید برای پایش نتایج آزمون در آزمایشگاه می‌باشند که استفاده از آنها در استاندارد ISO/IEC 17025:2017‌ و ISO 15189:2022 به منظور حصول اطمینان از اعتبار نتایج آزمون توصیه شده است. در آزمایشگاه‌های آزمون، کالیبراسیون و پزشکی به طور معمول از نمودار کنترل شوهارت برای پایش نتایج اندازه‌گیری استفاده می‌شود. نمودارهای کنترل شوهارت در پیاده‌سازی فاز یک نمودارهای کنترل بسیار مفید هستند. در این مرحله، فرایند اندازه‌گیری احیاناً به دلیل وجود انحراف‌های با دلیل بزرگ در پارامتر مورد نظر در حالت خارج از کنترل به سر می‌برند. از منظر تشخیصی نیز نمودارهای کنترل شوهارت می‌توانند با استفاده از اطلاعات موجود در روند مشاهدات نقش موثری را در ایجاد شرایط کنترل آماری برای فرایند ایفا کنند.

یکی از ضعف‌های اصلی نمودارهای کنترل شوهارت استفاده از اطلاعات موجود در آخرین نمونه مشاهده شده و نادیده گرفتن اطلاعات موجود در سایر نمونه‌ها است. این ویژگی باعث می‌شود نمودارهای کنترل شوهارت از حساسیت لازم برای شناسایی تغییرات کوچک در فرایند اندازه‌گیری نظیر 1.5σ یا کمتر برخوردار نباشند. برای رفع این نقطه ضعف از معیارهای دیگری نظیر حدود هشدار و قوانین حساس‌سازی نیز می‌توان در نمودارهای کنترل برای بهبود عملکرد آنها در مقابله با تغییرات کوچک استفاده شود. با این وجود سادگی و سهولت تفسیر نمودارهای کنترل شوهارت با اعمال این رویه‌ها کاهش یافته و متوسط طول تسلسل به طور قابل توجهی زمانی که فرایند اندازه‌گیری واقعاً تحت کنترل قرار دارد، کاهش می‌یابد. (متوسط تعداد نقاطی که تا قبل از مشاهده یک هشدار بر روی نمودار کنترل رسم می‌شود را متوسط طول تسلسل (average run length= ARL) می‌نامند. در صورت تمایل به شناسایی تغییرات کوچک در فرایند اندازه‌گیری در آزمایشگاه می‌توان از دو جایگزین بسیار موثر یعنی نمودارهای کنترل جمع تجمعی (‌CUSUM chart) و نمودار کنترل میانگین متحرک موزن نمایی (EWMA chart) استفاده نمود. در این پست قصد داریم کاربرد نمودارهای کنترل جمع تجمعی برای پایش اعتبار نتایج اندازه‌گیری در آزمایشگاه همراه با نحوه رسم این نمودار در نرم افزار Minitab را تشریح کنیم.

2- اصول بنیادی در رسم نمودارهای جمع تجمعی (CUSUM)

همانطور که گفته شد نمودارهای کنترل جمع تجمعی (‌CUSUM chart) نمودارهای خوبی برای کشف تغییرات کوچک در حد 1.5σ تا 2σ می‌باشند و در فرایندهای حساس مانند پایش نتایج اندازه‌گیری در مراکز آزمایشگاهی به کار می‌روند. از این نمودار در فاز 2 استفاده می‌شود. این نمودار برای کنترل انحراف مقادیر مشاهده شده که از نمونه‌ها بدست می‌آید با مقدار هدف یا مقدار مرجع (μ0) استفاده می‌شود. البته این نمودار هم همچون نمودار EWMA از اطلاعات گذشته اما این بار به صورت جمعی تجمعی استفاده می‌کند. به این صورت که اگر اندازه زیرگروه برابر یک باشد (مقادیر انفرادی)، به صورت زیر عمل می‌کند: 

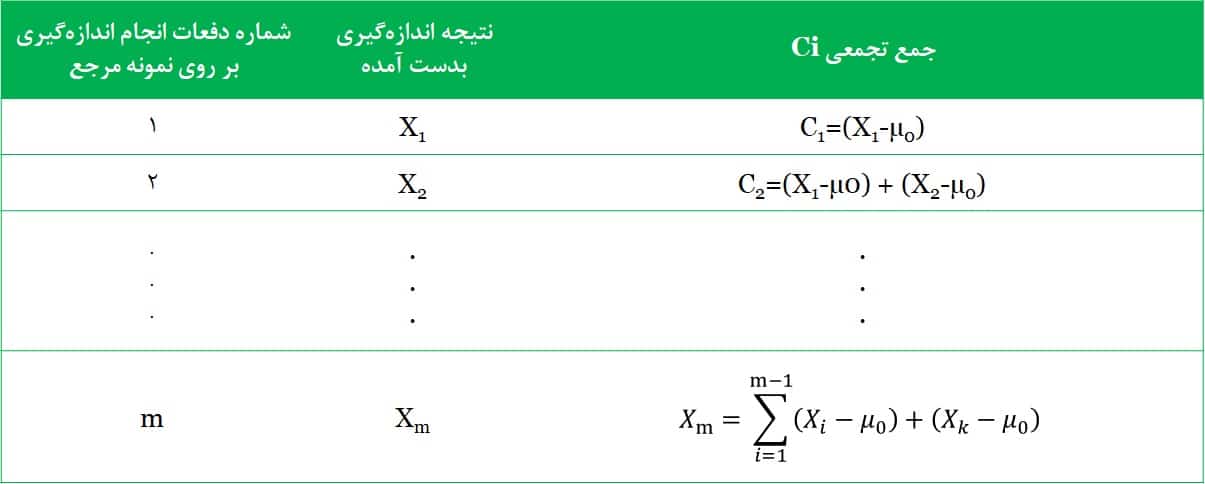
کارکنان آزمایشگاه از نمودارهای کنترل جمع تجمعی (CUSUM) می‌تواند برای پایش نتایج کنترل‌های میانی بر روی تجهیزات در آزمایشگاه استفاده کنند. نمودار جمع تجمعی با رسم جمع‌های تجمعی انحرافات مقادیر اندازه‌گیری شده از مقدار مرجع (μ0) مستقیماً از کلیه اطلاعات موجود در توالی مقادیر اندازه‌گیری استفاده می‌کند. به عنوان مثال فرض کنید تعداد تکرار اندازه‌گیری بر روی نمونه مرجع در هر دفعه انجام کنترل میانی تجهیزات برابر با n≥1 می‌باشد و X ̅_j نتایج دفعه jام انجام کنترل میانی را نشان می‌دهد. اگر مقدار مرجع (μ0) باشد آنگاه نمودار جمع تجمعی با رسم

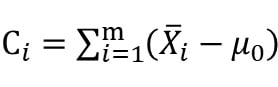
بر حسب شماره دفعه انجام کنترل میانی ایجاد می‌شود. کمیت Ci جمع تجمعی نامیده می‌شود که خود دفعه kام را نیز شامل می‌شود. نمودارهای کنترل جمع تجمعی در مقایسه با نمودارهای کنترل شوهارت به علت استفاده از اطلاعات چندین دوره نتایج بدست آمده از کنترل میانی تجهیزات نسبت به وجود تغییرات کوچک در میانگین سریع‌تر از خود واکنش نشان می‌دهند. به علاوه این نمودارها می‌توانند در زمانی که تعداد تکرار اندازه‌گیری در کنترل‌های میانی تجهیزات یک است (n-1) بسیار موثر باشند. این خاصیت نمودار کنترل جمع تجمعی از آن یک کاندید بسیار مفید برای استفاده در مراکز آزمایشگاهی که معمولاً از زیرگروه‌ها به اندازه یک (یک بار تکرار اندازه‌گیری بر روی نمونه‌های مرجع در کنترل‌های میانی) استفاده می‌شود و همچنین در فرایند ساخت قطعاتی که به طور مجزا تولید و به کمک یک سیستم اندازه‌گیری خودکار اندازه‌گیری می‌شود فراهم ساخته است.

نمودار CUSUM با رسم جمع‌هاي تجمعي مربوط به انحراف مقادير اندازه‌گیری شده از مقدار مرجع (μ₀) از تمام اطلاعات موجود در اندازه‌گیری‌های گذشته نيز استفاده مي‌كند. اگر میانگین نتایج اندازه‌گیری در سطح مقدار مرجع (μ₀) تحت کنترل باقی بماند آنگاه جمع تجمعی حاصل (C_i) یک فرآیند قدم زدن تصادفی با میانگین صفر خواهد بود.

اگر میانگین اندازه‌گیری بر روی نمونه مرجع مثلاً به μ₁ که (μ₁>μ₀) تغییر پیدا کند یک روند تدریجی بودی یا مثبت در جمع تجمع C_i ایجاد خواهد شد. در صورت افزايش در مقدار نتایج اندازه‌گیری‌ها بر روی نمونه مرجع:

If x_i>μ₀→C_i<C_i+1<C_i+2

و بر عکس اگر میانگین به مقدار اندازه‌گیری بر روی نمونه مرجع به μ₁ که (μ₁<μ₀) تغییر پیدا کند یک روند نزولی یا منفی ایجاد خواهد شد. در صورت كاهش در مقدار نتایج اندازه‌گیری‌ها بر روی نمونه مرجع:

If x_i< μ₀ →C_i>C_i+1>C_i+2

بنابراین اگر یک روند نزولی یا صعودی در نقاط رسم شده مشاهده شود باید آن را به عنوان یک تغییر در میانگین تلقی کرد و جستجو برای شناسایی انحراف با دلیل باید آغاز شود. 

3- تعیین معیار پذیرش (حدود کنترل) در نمودارهای جمع تجمعی

مطابق با بند 6-4-10 استاندارد ایزو 17025 “هرگاه بررسی‌های میانی برای حفظ اعتماد به عملکرد تجهیزات ضروری باشد، این بررسی‌ها باید طبق یک روش اجرایی انجام شود.” همچنین در استاندارد ایزو 17025 ذکر شده است که کارکنان آزمایشگاه پس از آن که فعالیت‌های کنترل کیفی را انجام دادند بایستی داده‌های بدست آمده از کنترل‌های میانی را تحلیل نمایند و برای کنترل و در صورت کاربرد، برای بهبود فعالیت‌های آزمایشگاه به کار گیرند. در صورتی که مشخص شود نتایج حاصل از تحلیل فعالیت‌های پایش، خارج از معیارهای از پیش تعریف شده است، باید اقدامات مناسب برای پیشگیری از گزارش نتایج غیر صحیح انجام شود. مطابق با آنچه که در استاندارد ایزو 17025 ذکر شده است در صورت استفاده از نمودارهای کنترل جمع تجعمی توسط کارکنان آزمایشگاه برای انجام فعالیت‌های کنترل کیفی بایستی معیار پذیرش یا همان حدود کنترلی را در نمودارهای جمع تجمعی مشخص نمایند. در نمودارهای کنترل جمع تجمعی از آن جاییکه در رابطه (X_i-μ₀) هر گونه تغییر کوچکی در نتایج اندازه‌گیری از مقدار مرجع باعث خارج از کنترل شدن فرآیند می‌شود، باید کاری کنیم تا نمودار تنها نسبت به تغییراتی واکنش نشان دهد و آنها را کشف کند که در حد معینی از حداکثر خطای مجاز (mpe) باشد که آن را با k نشان می‌دهیم. مثلاً برای کشف تغییراتی در حد 1σ ما k را نصف آن تعیین می‌کنیم یعنی (k=0.5) و به جای رابطه x_i-μ₀ از رابطه‌ی x_i-(μ₀+k) برای جمع‌های تجمعی استفاده می‌کنیم. از دیگر پارامترهای کلی که برای نمودار CUSUM می‌توان تعریف کرد، فاصله‌ی تصمیم‌گیری (Decision interval) یا همان h می‌باشد (h تقریباً همان حدود کنترل در CUSUM جمعی تجمعی یک طرفه می‌باشد. از h برای مشخص کردن وقوع وضعیت‌های خارج از کنترل استفاده می‌شود. معمولاً h مقداری بین 4σ≤h≤5σ می‌گیرد. هر چه قدر مقدار h و k را پایین‌تر انتخاب کنیم حساسیت بیشتری نسبت به تغییرپذیری فرآیند داریم، در برخی از مراجع توصیه شده است که h=4σ یا h=5σ و k=1.2σ در نظر گرفته شوند.

4- نمودار کنترل جمع تجمعی جدولی

نمودارهای جمع تجمعی را می‌توان به دو روش جدولی (الگوریتمی) و ماسک V ارائه کرد از بین این دو روش، روش جمع تجمعی جدولی ترجیح داده می‌شود در این پست روش تهیه و استفاده از نمودار جمع تجمع جدولی توضیح داده خواهد شد. در جمع تجمعی جدولی از آماره ⁺C برای انحراف‌ها در بالای μ₀ و از آماره ^–C برای انحراف‌ها در پایین μ₀ استفاده می‌شود آمارهای ⁺C و ^–C  را به ترتیب جمع جمعی بالا و پایین یک طرفه می‌نامند این آمار به صورت زیر محاسبه می‌شود:

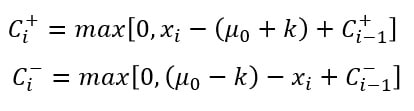
در رابطه‌های فوق، مقادیر شروع ⁺C و ^–C  برابر با صفر در نظر گرفته می‌شود. در این رابطه‌ها مقدار k غالباً مقداری بین مرجع μ₀ و مقدار خارج از کنترل میانگین نتایج اندازه‌گیری که بر اساس حداکثر خطای مجاز (MPE) تعیین می‌شود، در نظر گرفته می‌شود. مقدار K مقدار تغییری در میانگین است که علاقه‌مند، شناسایی سریع آن هستیم در نظر گرفته می‌شود. باید توجه داشت که ⁺C و ^–C  مقادیر انحراف از مقدار مرجع μ₀ که بزرگتر از K است را تجمیع می‌کند و مقادیر آنها در صورت منفی شدن برابر با صفر قرار داده خواهد شد. اگر مقادیر ⁺C و ^–C  از فاصله تصمیم‌گیری H بزرگتر شود آنگاه فرایند خارج از کنترل اعلام می‌شود.

5- رسم نمودار کنترل جمع تجمعی در نرم افزار minitab

در ادامه این پست همراه با یک مثال عددی نحوه رسم نمودارهای کنترل جمع تجمعی در نرم افزار minitab‌ نشان داده می‌شود. برای رسم نمودارهای کنترل بایستی کارکنان آزمایشگاه نمونه‌های مناسبی را انتخاب و استفاده نمایند. در پست آموزشی انواع نمونه ها برای رسم نمودار کنترل در آزمایشگاه شیمی نکات مفیدی در این خصوص ارائه شده است که بایستی به آنها قبل از شروع استفاده از نمودارهای کنترل استفاده گردد.

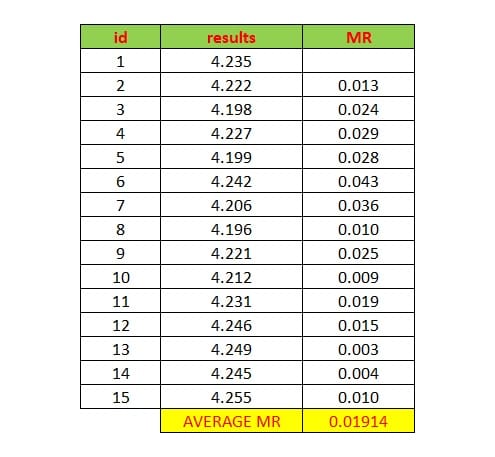
مثال: نتایج 15 دفعه آزمون بر روی یک نمونه مرجع با مقدار گواهی شده 4.21 مطابق با جدول زیر می‌باشد. می‌خواهیم با رسم یک نمودار جمع تجمعی هر گونه تغییری در نتایج اندازه‌گیری بیش از 1σ را مشخص نمایم.

گام 1: تعیین تخمین انحراف استاندارد نتایج ( σ= R̅/d₂)

n=2

d₂ = 1.128

σ= R̅/d₂ = 0.01914/1.128 = 0.0169

مقدار d2 برای سایر اندازه‌ زیر گروه‌ها بر اساس جدول زیر تعیین می‌شود.

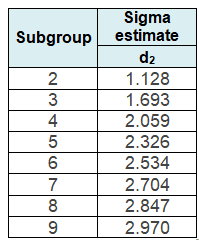
گام دوم: تعیین مقدار انحراف مجاز 

(K= 0.5 σ = 0.5*0.0169 = 0.00848) 

گام سوم: محاسبه بازه تصمیم (h)

این مقدار معمولاً به صورت زیر تعیین می‌شود.

± 4 σ = ± 4 * 0.0169= ± 0.0679

UCL = +0.0679 and LCL = -0.00679

گام چهارم: محاسبه مقادیر جمع تجمعی بالا و پایین

مقادیر جمع تجمعی بالا و پایین برای هر نتیجه اندازه گیری بدست آمده به صورت زیر محاسبه می‌شود. در رابطه زیر i نشان دهنده دفعه اندازه‌گیری است.

Target value =4.21

Upper CUSUM (UC_i)= Max[0, UC_i-1+x_i – Target value-k)

Lower CUSUM (LC_i)= Min[0, LC_i-1+x_i – Target value+k)

برای اولین نتیجه اندازه گیری بدست آمده 4.235:

Upper CUSUM (UC₁)= Max[0, 0+4.235– 4.21-0.0084) =0.017

Lower CUSUM (LC₁)= Min[0, 0+4.235-4.21+0.00848) = 0

برای دومین نتیجه اندازه گیری بدست آمده 4.222

Upper CUSUM (UC₁)= Max[0, 0.017+4.222– 4.21-0.0084) =0.02

Lower CUSUM (LC₁)= Min[0, 0+4.222-4.21+0.0084) = 0

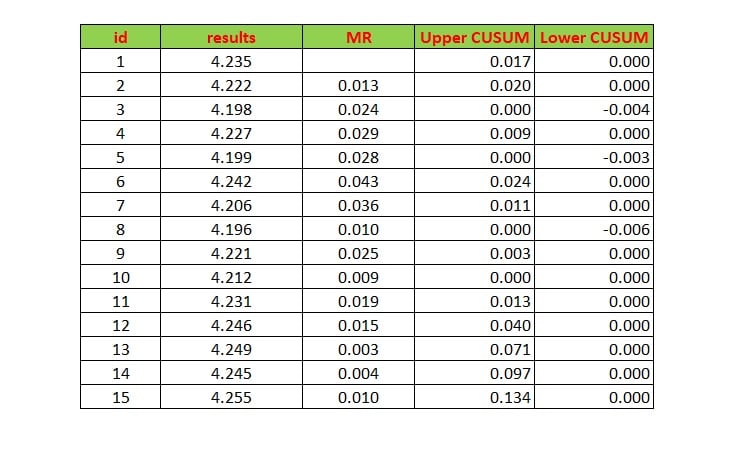
به طور مشابه برای سایر نتایج اندازه‌گیری حدود بالا و پایین جمع تجمعی محاسبه می‌شود. نتایج این محاسبات برای مثال ارائه شده به صورت جدول زیر می‌باشد.

گام پنجم: حدود تصمیم‌گیری یا حدود کنترل (UCL and LCL) و همچنین رسم مقادیر UC_i & LC_i بر روی نمودار 

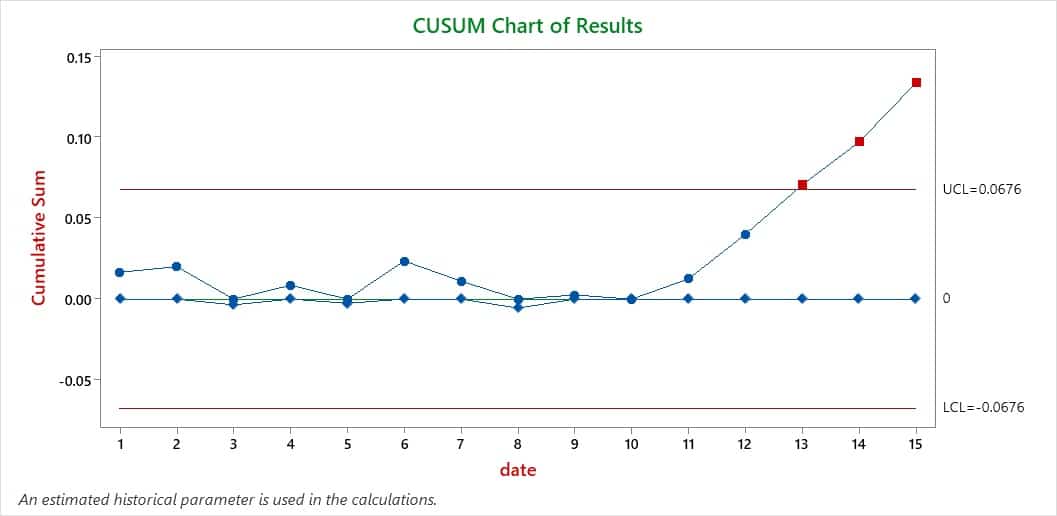
گام ششم: نتیجه‌گیری

اگر تمامی نقاط رسم شده بر روی نمودار در محدود (UCL and LCL) باشند فرایند اندازه‌گیری در حال حاضر تحت کنترل است. در نمودار جمع تجمعی CUSUM رسم شده برای مثال ارائه شده نشان می‌دهد که از نقطه 13 به بعد فرایند اندازه‌گیری خارج از کنترل است و کارکنان آزمایشگاه بایستی علت ریشه‌ای آن را شناسایی نمایند و پس از انجام اقدامات اصلاحی لازم مجددا وضعیت فرایند را با تکرار آزمون بر روی نمونه مرجع بررسی نمایند.