انتخاب تکنیک مناسب برای رسم منحنی کالیبراسیون در آزمایشگاه
فهرست محتوایی مقاله
Toggle1- مقدمهای بر رسم منحنی کالیبراسیون
منحنی کالیبراسیون یا منحنی استاندارد یکی از تکنیکهای رایج و مهم در آزمایشگاه شیمی میباشد، که در آن با اندازهگیری سیگنال (عدد جذب، عدد نشر، سطح زیر پیک و …) برای نمونه مجهول و مقایسه آن با سیگنال نمونههای معلوم (نمونههای مرجع) غلظت نمونه مجهول تعیین میگردد. منحنی کالیبراسیون بیانگر رابطهی بین نشاندهی و مقدار کمیت اندازهگیری شده متناظر با آن است. به منظور بدست آوردن یک نتیجه اندازهگیری درست در آزمایشگاه برای یک نمونه مجهول با استفاده از منحنی کالیبراسیون، نکات زیادی وجود دارد که بایستی توسط کارکنان آزمایشگاه در نظر گرفته شوند. یکی از مهمترین آنها انتخاب تکنیک مناسب برای رسم منحنی کالیبراسیون میباشد بر این اساس در این پست آموزشی ابتدا به معرفی انواع روشها و تکنیکهای کالیبراسیون تک نقطهای، چند نقطهای و براکتینگ میپردازیم، سپس بیان خواهیم کرد که چه زمانی کارکنان آزمایشگاه میتوانند از هر یک از این روشها برای رسم منحنی کالیبراسیون تجهیزات اندازهگیری خود استفاده نمایند. همچنین برخی از نکات مهمی که بایستی هنگام رسم منحنی کالیبراسیون در آزمایشگاه در نظر گرفته شود، را نیز در این پست ذکر خواهیم میکرد.

2- اصطلاحات و تعاریف در رسم منحنی کالیبراسیون
2-1- نمودارکالیبراسیون (Calibration diagram): بیان گرافیکی رابطهی بین نشاندهی و نتیجه اندازهگیری متناظر با آن است. یک نمودار کالیبراسیون به صورت نواری از یک صفحه است که توسط محورهای نشاندهی و نتیجه اندازهگیری تعریف میشود و بیانگر رابطهای بین یک نشاندهی و یکسری مقادیر کمیت اندازهگیری شده است. یک رابطه یک به چند ارایه شده است و عرض نوار مربوط به نشاندهی، بیانگر عدمقطعیت اندازهگیری دستگاهی است. بیانهای دیگر برای این رابطه، شامل منحنی کالیبراسیون و عدمقطعیت اندازهگیری آن، جدول کالیبراسیون و یا مجموعهای از توابع است. زمانی این مفهوم به کالیبراسیون مربوط میشود که عدمقطعیت اندازهگیری دستگاهی در مقایسه با عدمقطعیتهای مربوط به مقادیر کمیت استانداردهای اندازهگیری بزرگ باشد.
2-2- منحنی کالیبراسیون (Calibration curve): بیان رابطهی بین نشاندهی و مقدار کمیت اندازهگیری شده متناظر با آن است. منحنی کالیبراسیون بیان یک رابطهی یک به یک است به طوری که نتیجه اندازهگیری هیچ اطلاعاتی درباره عدمقطعیت اندازهگیری ندارد.
2-3- خطیبودن (Linearity): توانایی روش در به دست آوردن سیگنالهای که مستقیماً به مقدار اندازهگیری شده در نمونه متناسب است.
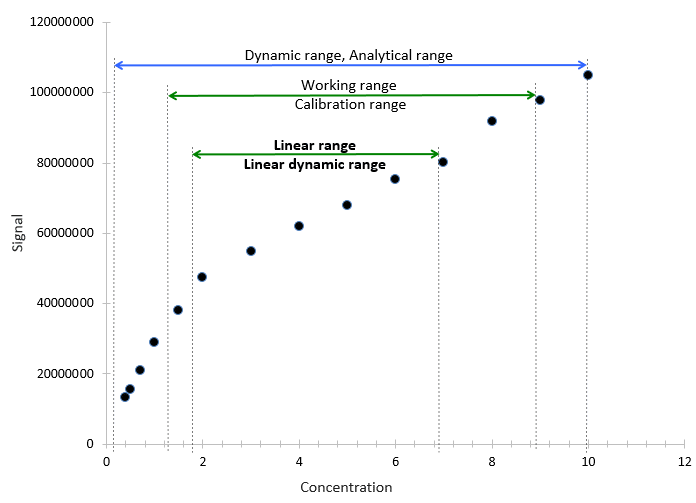
2-4- محدوده خطیبودن (Linearity Range): محدوده از گستره اندازهگیری که در آن سیگنال به طور مستقیم به مقدار اندازهگیری شده در نمونه متناسب است.
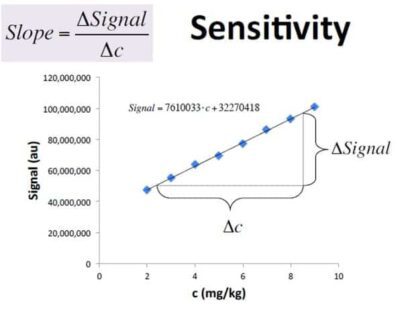
2-5- حساسیت (Sensitivity): میزان تغییرات در پاسخ اندازهگیری شده به نسبت تغییرات ایجاد شده در مقدار اندازهگیری شده، میباشد. حساسیت شیب منحنی کالیبراسیون میباشد. اگر محور X و Y هم واحد باشند، روشی که مقدار حساسیتش به یک نزدیک تر است مطلوب تر است. اگر محور X و Y هم واحد نباشند، روشی که دارای شیب بزرگی باشد، توانایی بهتری برای تفکیک تفاوتهای کوچک مقادیر اندازهگیری شده از یکدیگر دارد. هرچه حساسیت (شیب منحنی کالیبراسیون) بزرگتر باشد، توانایی روش در تشخیص تغییرات کوچک ایجاد شده در مقدار اندازهگیری شده بر روی یک نمونه بیشتر است.
2-6- ماده مرجع (Reference material): مادهای که در خصوص خصیصههای مشخص به کفایت همگن و پایدار که برای استفاده مورد نظر در اندازهگیری یا امتحان خصیصههای نامی مشخص شده، مناسب است.
3- اصول کلی رسم منحنی کالیبراسیون
کالیبراسیون روش اجرایی است که تفاوت سیستماتیکی را تعیین میکند که ممکن است بین سیستم اندازهگیری و سیستم “مرجع” بیان شده با مواد مرجع و مقادیر پذیرفته آنها، وجود داشته باشد. در این پست آموزشی اصطلاح سیستم (سیستم اندازهگیری یا سیستم مرجع) نه تنها برای بیان دستگاه اندازهگیری به کار برده میشود بلکه مجموعه روشهای اجرایی، اپراتورها و شرایط محیطی مرتبط با آن دستگاه را نیز بیان میکند.
خروجی روش اجرایی کالیبراسیون تابع کالیبراسیون است که برای تبدیل نمودن نتایج اندازهگیری بعدی مورد استفاده قرار میگیرد. در این پست آموزشی اصطلاح ”تبدیل” به موارد زیر اشاره دارد:
- تصحیح نتایج اندازهگیری بعدی در صورتی که هر دو، مقادیر مرجع و مقادیر نشانداده شده توسط دستگاه واحدهای اندازهگیری یکسان داشته باشند (محور x و y هم واحد هستند)؛
- انتقال از واحدهای اندازهگیریهای مشاهده شده به واحدهای اندازهگیری نمونههای مرجع اشاره میکند وقتی که محور x و y در رسم منحنی کالیبراسیون هم واحد نیستند.
اعتبار تابع کالیبراسیون به دو شرط زیر بستگی دارد:
- اندازهگیریهایی که از آنها تابع کالیبراسیون محاسبه شده است نشانگر شرایط عادی باشند که تحت آن سیستم اندازهگیری کار میکند، و
- سیستم اندازهگیری در حالت کنترل باشد.
آزمایش کالیبراسیون باید برای حصول اطمینان از اینکه نکته الف) برآورده میشود، طراحی شود. روش کنترلی در سریعترین زمان ممکن، زمانی را که سیستم باید خارج از کنترل مورد ملاحظه قرار گیرد، تعیین میکند.
روش اجرایی در این پست آموزشی فقط برای سیستمهای اندازهگیری که به طور خطی با سیستمهای مرجعشان مرتبط هستند، کاربرد دارد. برای بررسی اینکه آیا فرض خطیبودن معتبر است، بیش از دو نمونه مرجع باید در طی آزمایش کالیبراسیون مورد استفاده قرار گیرد. با استفاده از چندین نمونه مرجع، روش پایه استراتژی و تکنیکهایی را برای تحلیل دادههای جمعآوری شده در طی آزمایش کالیبراسیون فراهم میکند. اگر خطیبودن مورد بحث نباشد، آنگاه روشی جایگزین سادهتر از روش پایه میتواند جهت برآورد تابع کالیبراسیون خطی بر اساس تک نقطهای مورد استفاده قرار گیرد. اگر خطیبودن مورد تایید نشده باشد، آنگاه روش جایگزین دوم به نام یعنی ”روش براکتینگ” میتواند برای ترسیم منحنی کالیبراسیون استفاده شود.
روش پایه (کالیبراسیون چند نقطهای) و روش تک نقطهای بر اساس این فرض هستند که تلاش صرف شده در کالیبراسیون طی دوره پایداری فرآیند معتبر خواهد بود. جهت مطالعه این دوره در مدتی که کالیبراسیون معتبر است، روش کنترلی باید مناسب باشد. روش کنترلی برای پی بردن به اینکه آیا تغییراتی که بررسی و /یا کالیبراسیون مجدد را توجیه میکنند در سیستم رخ دادهاند، طراحی شده است. روش کنترلی همچنین راهی ساده برای تعیین دقت مقادیری که با تابع کالیبراسیون معین تبدیل یافتهاند، فراهم میسازد.
روش براکتینگ پر زحمت میباشد اما میتواند درستی بهتری در تعیین مقادیر کمیتهای مجهول فراهم کند. این روش از احاطه هر چه تنگ تر (براکتینگ) هر کمیت مجهول با دو نمونه مرجع و استخراج مقدار تبدیل یافته برای کمیت مجهول از اندازهگیریهای هم کمیت مجهول و هم مقادیر دو نمونه مرجع، تشکیل میشود. فقط پایداری فرآیند اندازهگیری کوتاه مدت فرض شود (پایداری طی اندازهگیری کمیت مجهول و دو نمونه مرجع) حالت خطی فقط در بازه بین مقادیر دو نمونه مرجع فرض شود.
4- روش کالیبراسیون چند نقطهای (روش پایه)
4-1- کلیات روش کالیبراسیون چند نقطهای
این بند چگونگی برآورد و استفاده از تابع کالیبراسیون خطی را زمانی که چندین (بیش از دو) نمونه مرجع در دسترس باشند، شرح می دهد. در دسترس بودن چندین نمونه مرجع امکان میدهد که حالت خطی تابع کالیبراسیون تصدیق شود.
4-2- فرضیات روش کالیبراسیون چند نقطهای
هنگام بررسی و صحهگذاری منحنی کالیبراسیون چهار فرضیه زیر مورد بررسی قرار میگیرند:
- یکسان بودن واریانس دادههای (یا باقیماندهها) در کل گستره اندازهگیری؛
- استقلال دادههای اندازهگیری (یا باقیماندهها) در طول به زمان؛
- نرمال بودن تابع توزیع نتایج (یا باقیماندهها)؛
- خطیبودن منحنی کالیبراسیون؛
برای بررسی این فرضیهها به طور معمول از ارزیابی باقیماندهها (Residuals) نسبت به گستره اندازهگیری و یا ارزیابی باقیماندهها نسبت به زمان بجای ارزیابی چشمی استفاده میشود.
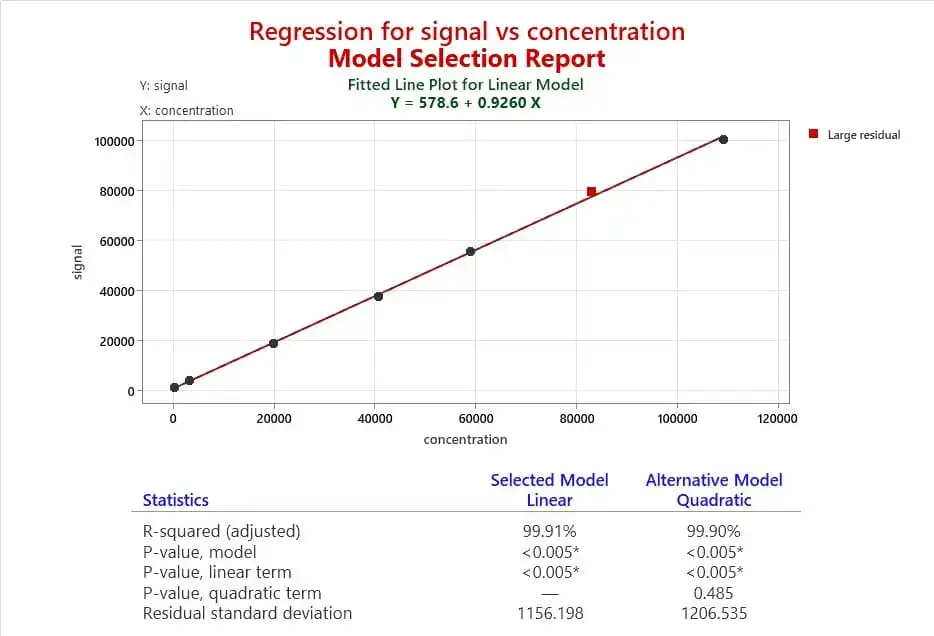
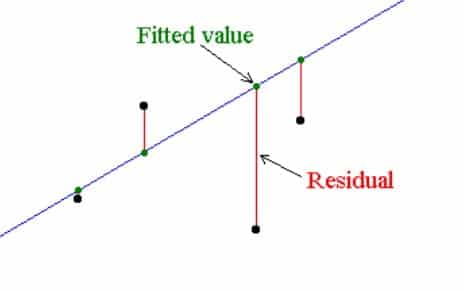
باقیماندهها: اختلاف بین مقدار مشاهده شده و مقدار محاسبه شده با استفاده از معادله خط میباشد. باقیماندهها نشاندهنده میزان تناسب خط با دادهها میباشند. خطی که دارای کوچکترین مجموع مربعات باقیماندهها باشد، بهترین خط برای نمایش ارتباط خطی بین متغیرهای x و y میباشد. به همین دلیل این نوع از رگرسیون را “رگرسیون کمترین مربعات (OLS)” مینامند. در این روش معادله خط طوری تعیین میشود که مجموع توانهای دوم انحرافات عمودی از خط حداقل شود.
مهمترین فرضیات که هنگام ارزیابی منحنی کالیبراسیون بررسی میشوند عبارتند از:
- فرض میشود که هیچ خطایی در مقادیر پذیرفته نمونههای مرجع وجود ندارد. در عمل، مقادیر پذیرفته برای نمونههای مرجع همراه با عدمقطعیتهایشان بیان میشوند. فرض نبود خطا در مقادیر پذیرفته نمونههای مرجع در صورتی میتواند معتبر در نظر گرفته شود که عدمقطعیتها در مقایسه با بزرگی خطاهای موجود در مقادیر اندازهگیری شده این نمونههای مرجع کوچک باشند.
- تابع کالیبراسیون فرض میشود که خطی باشد (این فرض بایستی بررسی شود).
- اندازهگیریهای گزارش شده برای یک نمونه مرجع معین، فرض میشوند که دارای توزیع مستقل و نرمال باشند، با واریانس اشاره شده به عنوان ”واریانس باقیماندهها” (نحوه بررسی فرضها مستقل و نرمالبودن در پست آموزشی بعدی تشریح خواهند شد). ریشه دوم واریانس باقیماندهها به انحراف معیار باقی ماندهها اشاره می کند.
- فرض میشود که انحراف معیار باقی ماندهها نسبت به مقدار پذیرفته نمونههای مرجع ثابت یا نسبی باشد.
برقرار بودن یا نبودن هر یک از این فرضیهها فوق میتواند تکنیک آماری که برای بدست آوردن منحنی کالیبراسیون مورد استفاده قرار میگیرد را تحت تاثیر قرار دهد. به عنوان مثال اگر باقیماندهها در گستره اندازهگیری ثابت باشند از منحنی کالیبراسیون حداقل مربعات معمولی (OLS) استفاده میشود و غیر است صورت از منحنی حداقل مربعات وزنی (WLS) استفاده میشود. در تصویر زیر نیز برخی از مهمترین فرضیات که در منحنی باقیماندهها به گستره کاری بررسی میشوند را نشان میدهد. در این نمودار باقیماندهها به گستره اندازهگیری یا نمودار باقیماندهها به زمان اگر بعضی از دادهها شک بر انگیز باشند یا اگر روند زمانی مشهود باشد، آنگاه تحقیق و بررسی برای یافتن علل بی نظمیها باید صورت گیرد. به محض اینکه علل بی نظمیها بر طرف شوند، آزمایش کالیبراسیون بایستی تکرار شود و دادههای جدید بایستی برای تحقق متحی کالیبراسیون گردآوری شوند. همچنین این نمودار ابزاری قدرتمند برای آشکارسازی انحراف از دو فرض حالت خطی و انحراف معیار ثابت باقیماندهها میباشد.
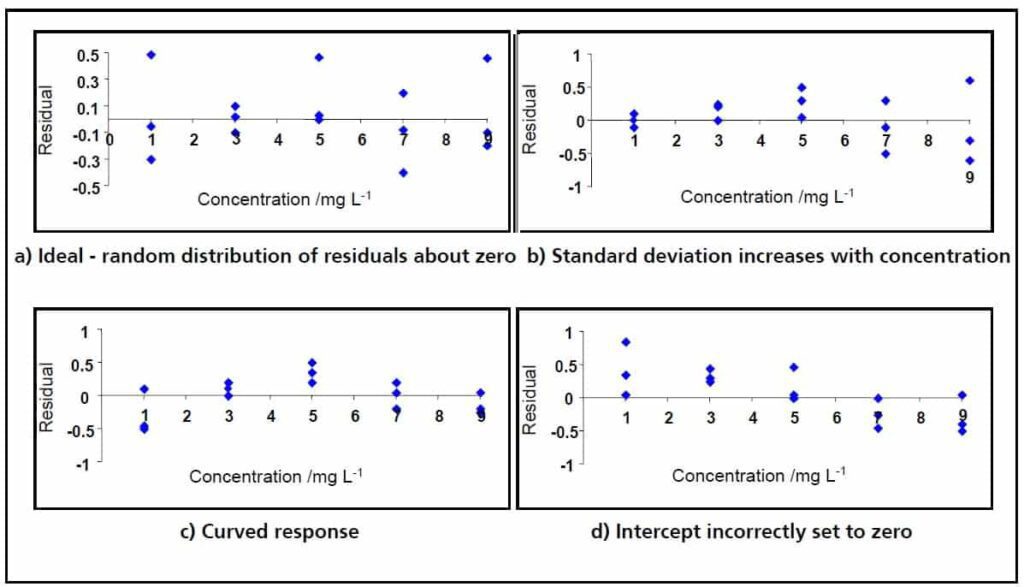
4-3- آزمایش کالیبراسیون به روش چند نقطهای
4-3-1- شرایط آزمایش
شرایط آزمایش بایستی همان شرایط بهرهبرداری عادی سیستم اندازهگیری باشد؛ یعنی اگر برای مثال بیش از یک اپراتور تجهیزات اندازهگیری را به کار میبرد آنگاه بایستی بیش از یک اپراتور در آزمایش کالیبراسیون حضور داشته باشد.
4-3-2- انتخاب نمونههای مرجع (RMs)
گستره مقادیر که با نمونههای مرجع انتخاب شده انتخاب شده پدید آمده است بایستی (تا آنجا که ممکن است) گستره مقادیر مواجه شده طی شرایط بهرهبرداری عادی سیستم اندازهگیری را در بر گیرد. ترکیب نمونههای مرجع انتخاب شده بایستی هر چه نزدیکتر به ترکیب ماده نشان شده برای اندازهگیری باشد. مقادیر نمونههای مرجع بایستی تقریباً به طور هم فاصله بر روی گستره مقادیر مواجه شده در جریان شرایط بهرهبرداری عادی سیستم اندازهگیری، توزیع شوند.
4-3-3- تعداد نمونههای مرجع برای رسم منجنی کالیبراسیون
تعداد نمونههای مرجع مورد استفاده جهت ارزیابی تابع کالیبراسیون بایستی حداقل ٣ باشد. برای ارزیابی اولیه تابع کالیبراسیون تعدادی بزرگتر از ٣ توصیه میشود (حداقل ٣ بر روی زیر بازهای که در آن درباره خطی بودن تابع کالیبراسیون تردید وجود دارد).
4-3-4- تعداد تکرارها بر روی هر نمونه مرجع
هر نمونه مرجع بایستی حداقل دو بار اندازهگیری شود (در عمل هر چند تا تکرار که ممکن باشد توصیه می شود). تعداد تکرارها بایستی برای همه نمونههای مرجع یکسان باشد. زمان و شرایط در تکرارهایی که اتخاذ شدهاند بایستی هر پهنای گسترهای که لازم است را پوشش دهد تا از این که همه شرایط بهرهبرداری نشان داده میشوند، اطمینان حاصل شود.
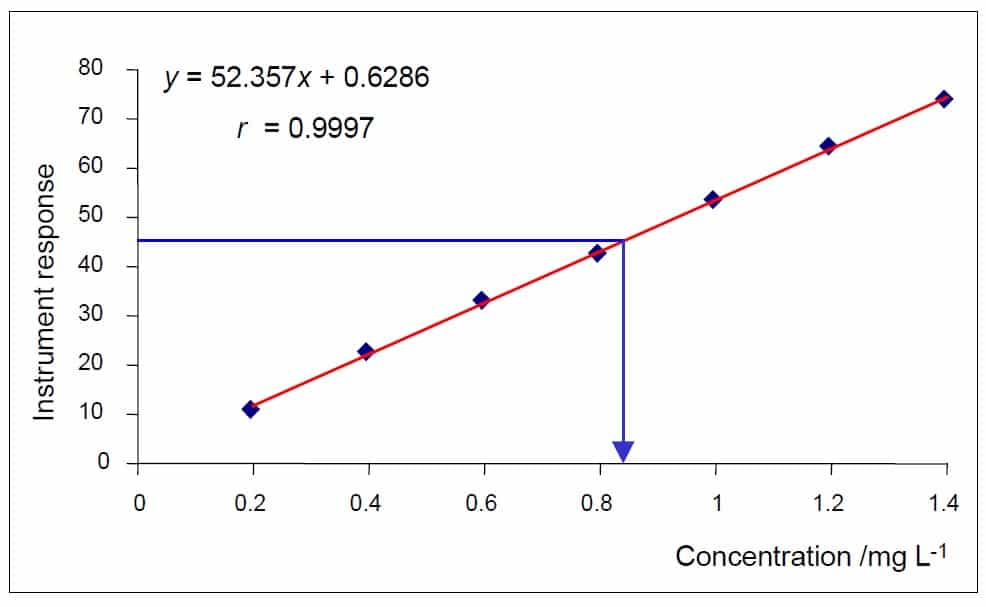
4-4- استراتژی برای تحلیل دادهها
دادهها را جهت کنترل موارد زیر به صورت نمودار نشان دهید:
- حالت کنترل سیستم اندازه گیری طی آزمایش کالیبراسیون؛
- فرض خطی بودن؛ و
- تغییرپذیری اندازهگیریها به عنوان تابع مقادیر پذیرفته نمونههای مرجع.
تابع کالیبراسیون خطی را بنا بر فرض انحراف معیار ثابت باقی ماندهها برآورد نمایید. تابع کالیبراسیون خطی و باقیماندهها را بر روی نمودار نشان دهید. نمودار باقیماندهها نشان دهنده قوی انحراف از فرض خطی بودن یا از فرض انحراف معیار ثابت باقیماندهها میباشد. اگر فرض انحراف معیار ثابت باقیماندهها صدق کند، از روش حداقل مربعات معمولی (OLS) برای رسم منحنی کالیبراسیون استفاده میشود. اگر انحراف معیار ثابت باقیماندهها رد شوید از روش حداقل مربعات وزنی (WLS) استفاده میشود و تابع کالیبراسیون خطی را بنا بر فرض انحراف معیار نسبی باقیماندهها برآورد نمایید و تابع کالیبراسیون و باقیماندهها را بر روی نمودار نشان دهید.
فقدان برازش تابع کالیبراسیون (lack of fit) را ارزیابی نمایید. اگر تغییرپذیری به سبب فقدان برازش نسبت به تغییرپذیری به علت تکرار اندازهگیریها بزرگ باشد، روشهای اجرایی دنبال شده در جریان آزمایش کالیبراسیون را بررسی نمایید و فرض خطیبودن تابع کالیبراسیون را دوباره امتحان نمایید. اگر فرض خطیبودن صدق نکند، آنگاه چاره کار استفاده از روش براکتینگ میباشد. در نهایت پس از بدست آوردن یک منحنی کالیبراسیون مطلوب میتوانیم با استفاده از آن مقادیر اندازه گیری شده برای سیگنال نمونههای مجهول را با تابع کالیبراسیون به غلظت تبدیل نمایید.
برای آشنایی با نحوه رسم منحنی کالیبراسیون چند نقطهای در نرم افزار Minitab میتوانید فیلم آموزشی قرارداده شده در پست چگونه عدم قطعیت خطی بودن را می توان محاسبه کرد؟ را مشاهده نمایید.
5- دو روش جایگزین برای روش منحنی کالیبراسیون چند نقطهای
تحت شرایط خاص، دو روش جایگزین میتواند برای کالیبره فرآیند اندازهگیری استفاده شود. این دو روش در واقع موارد خاصی از روش پایه هستند که در آنها فقط یکی از دو نمونه مرجع استفاده میشود. روش کالیبراسیون تک نقطهای تکنیک سریعی است که به شخص اجازه میدهد تا سیستم اندازهگیری را هنگامی که هیچ تردیدی درباره خطیبودن تابع کالیبراسیون وجود ندارد، “دوباره کالیبره” نماید. روش جایگزین دیگر برای رسم منحنی کالیبراسیون روش براکتینگ است. روش براکتینگ تکنیکی کاربردی است که تعیین مقدار کمیت مجهول را با دقت بالا و با حداقل مجموعه فرضها، ممکن میسازد.

5-1- روش کالیبراسیون تک نقطهای (One-Point calibration method)
این روش برای کالیبراسیون مجدد سریع هنگامی که هیچ تردیدی درباره خطیبودن تابع کالیبراسیون بر روی گستره معین وجود ندارد، مفید میباشد. برای حصول اطمینان از اینکه کمیت مجهول با مقدار حقیقی صفر به همان اندازه صفر اندازهگیری شود،”نقطه صفر” به وسیله تنظیم برخی از صفحههای مدرج به دست آورده شود. فقط یک نمونه بلانک (کمیت با مقدار حقیقی صفر) و یک نمونه مرجع در این روش استفاده شود. میتواند یادآوری شود که از نظر پیشینه این روش، کالیبراسیون تک نقطهای نامیده شده است اما در واقع کالیبراسیون دو نقطهای انجام شده با یک نمونه بلانک و یک نمونه مرجع میباشد. این به اصطلاح ” کالیبراسیون تک نقطهای” به دلیل حالت تردید در نقطه صفر، روشی ضعیف و نامطمئن میباشد. این روش نبایستی برای مقاصد کالیبراسیون توصیه شود اما اصولاً برای کنترل تابع کالیبراسیون خطی موجود توصیه میشود.
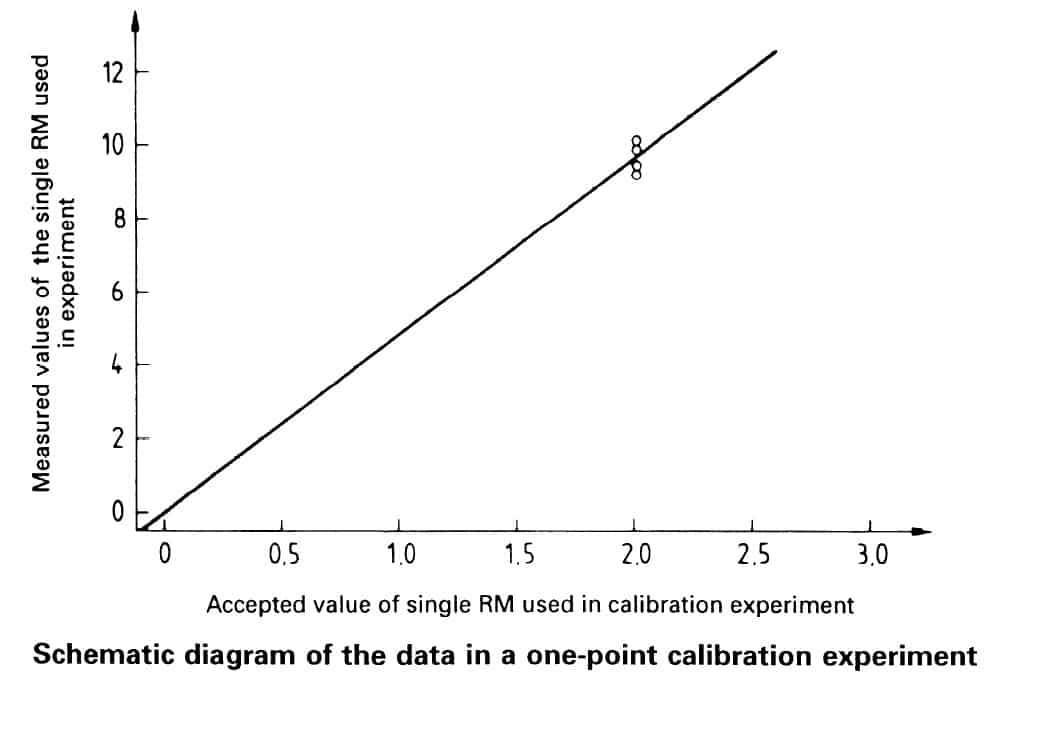
5-1-1- فرضیههای روش کالیبراسیون تک نقطهای
- هیچ خطایی در مقدار پذیرفته شده تک نمونه مرجع و نمونه بلانک استفاده شده با این روش وجود ندارد (فرض آزمون نشده است)؛
- تابع کالیبراسیون بر روی گستره خطی است (فرض آزمون نشده است)؛
- انحراف معیار باقیماندهها ثابت است (فرض آزمون نشده است)؛
5-1-2- آزمایش کالیبراسیون تک نقطهای
الف) شرایط آزمایش: شرایط آزمایش بایستی همان شرایط بهرهبرداری عادی سیستم اندازهگیری باشد.
ب) انتخاب نمونه مرجع: تک نمونه مرجع به کار رفته در آزمایش بایستی مقدار پذیرفته شدهای بزرگتر (تا آنجا که ممکن است) از مقادیر مواجه شده طی شرایط عادی سیستم اندازهگیری داشته باشد.
ج) تعداد تکرارها نمونه مرجع: نمونه مرجع بایستی حداقل دو بار اندازهگیری شود.
5-2- روش کالیبراسیون براکتینگ (Bracketing technique)
این روش زمانی که درباره خطی بودن تابع کالیبراسیون بر روی گستره کامل مقادیر مواجه شده در طی بهرهبرداری عادی سیستم اندازهگیری تردید وجود دارد، سودمند است. این روش زمانی که درباره پایداری فرایند اندازهگیری نگرانی وجود داشته باشد نیز سودمند است. قاعده کلی این روش کاهش هر چه بیشتر بازهای است که بر روی آن خطیبودن تابع کالیبراسیون فرض شده است. این امر به احاطه هر چه تنگتر (یا براکتینگ) مقدار کمیت مجهول توسط دو مقدار از مواد مرجع منتهی میشود. به دلیل احاطه تنگ هر کمیت مجهول توسط دو نمونه مرجع و به دلیل دوره کوتاه زمانی مورد نیاز برای این روش اجرایی (زمان برای اندازهگیری کمیت مجهول و دو نمونه مرجع، تکنیک براکتینگ موجب درستی بیشتری در تعیین مقدار تبدیل یافته کمیت مجهول میشود. کمیت مجهول و دو نمونه مرجع با هم اندازهگیری میشوند. مقدار کمیت مجهول به طور مستقیم بر مبنای درونیابی خطی میان دو مقدار معلوم نمونههای مرجع برآورد میشود.
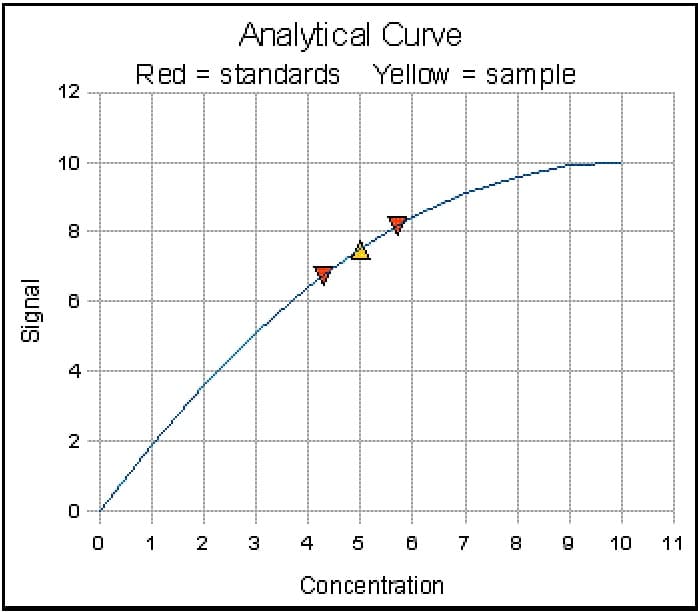
5-2-1- فرضیههای روش براکتینگ
برای اینکه فقط دو نمونه مرجع مورد استفاده قرار میگیرد تکنیک براکتینگ کنترل هیچ کدام از فرضهای زیر را مد نظر قرار نمیدهد:
- اینکه هیچ خطایی در مقادیر پذیرفته شده نمونههای مرجع وجود ندارد؛
- اینکه تابع کالیبراسیون در میان دو نمونه مرجع خطی است؛
- اینکه انحراف معیار باقیماندهها ثابت است.
5-2-2- آزمایش براکتینگ
الف) شرایط آزمایش: شرایط آزمایش بایستی به نحوی باشد که تغییرپذیری در میان اندازهگیریهای نمونههای مرجع یکسان تا حد امکان کوچک باشد.
ب) انتخاب نمونههای مرجع (RMs): گستره مقادیر پدید آمده به وسیله دو نمونه مرجع بایستی تا حد امکان کوچک باشد و باید مقدار کمیت مجهولی که باید مورد اندازهگیری قرار گیرد را شامل شود.
ج) تعداد نمونههای مرجع (RMs): برای هر کمیت مجهول دو نمونه مرجع مورد استفاده قرار میگیرد.
د) تعداد تکرارها: هر دو نمونه مرجع و کمیت مجهول بایستی حداقل دو بار اندازهگیری شوند.
6- سخن پایانی
در این پست آموزشی به معرفی انواع منحنی کالیبراسیون تک نقطهای، براکتنیگ و چند نقطهای پرداختیم و کاربردهای یک از آنها را در آزمایشگاه تشریح نمودیم. در صورت وجود هر گونه پرسشی در خصوص رسم منحنی کالیبراسیون در آزمایشگاه میتوانید سوالات خود را در قسمت کامنتهای این پست قرار دهید. سعی خواهد شد تا جای ممکن به سئوالات مطرح شده پاسخ مناسب داده شوند. همچنین در صورت نیاز به برگزاری دوره آموزشی صحه گذاری روشهای آزمون با نرمافزار Minitab برای کارکنان آزمایشگاه یا برای دریافت خدمات مشاوره برای اخذ گواهینامه ایزو 17025 و مشاوره ایزو 15189 میتوانید با ما تماس بگیرید.




دیدگاهتان را بنویسید