چگونگی بررسی تفاوت معنادار آماری در دو معادله رگرسیون خطی
فهرست محتوایی مقاله
Toggle1- مقدمه
اگر آنالیز رگرسیون خطی را انجام دهید، ممکن است به مقایسه عرض از مبداء و شیب خطوط رگرسیون های متفاوت نیاز داشته باشید. تصور کنید یک رابطه بین X و Y وجود دارد. حال فرض کنید که میخواهید تعیین کنید آیا این تفاوت معنادار آماری در دو معادله رگرسیون تحت شرایط متفاوت وجود دارد یا نه؟ این شرایط متفاوت میتواند دو محیط متفاوت، دو روش آزمون متفاوت، دو فرایند تولیدی متفاوت، دو اپراتور متفاوت یا متغیرهای کیفی مشابه دیگر باشند که میخواهید تعیین کنید که رابطه بین X و Y تحت تاثیر این متغیرهای کیفی متفاوت قرار گرفته است یا خیر.
به عنوان مثال شما ممکن است بخواهید ارزیابی کنید که آیا رابطه قد و وزن بازیکنان فوتبال با رابطه قد و وزن افراد عادی در جامعه از نظر آماری تفاوت معناداری دارد یا خیر؟
شما می توانید به صورت چشمی عرض از مبداء و شیب خطوط رگرسیون را با هم مقایسه کنید. با این حال، باز هم نیاز به انجام آزمونهای آماری جهت بررسی وجود تفاوت معنادار است. آزمونهای فرض آماری کمک خواهند کرد که تفاوتهای واقعی را از تفاوتهای ناشی از خطای نمونه برداری در یک سطح اطمینان مشخص، تعیین کنید.
در این پست، نشان داده خواهد شد که چگونه میتوان رابطههای بین مدلهای مختلف رگرسیون را با هم مقایسه کرد و وجود یا عدم وجود تفاوت معنادار آماری را تعیین نمود. خوشبختانه این آزمونها به راحتی با نرم افزار آماری Minitab قابل انجام است.
برای انجام این کار در این پست از یک مثال استفاده شده است (دانلود فایل مثال) که در آن دو متغیر ورودی و خروجی در یک فرایند فرضی وجود دارند. قرار است رابطه بین این دو متغیر را در دو شرایط متفاوت (به عنوان مثال دو روش آزمون متفاوت) با هم مقایسه شوند.
2- مقایسه عرض از مبدا دو خط در آنالیز رگرسیون ها
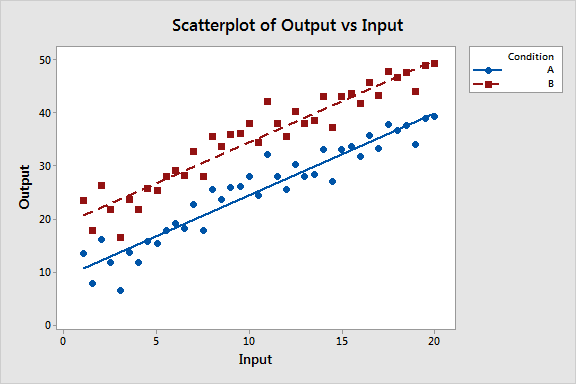
هنگامی که عرض از مبداء در دو معادله رگرسیون مختلف متفاوت است، نشان دهنده آن است که دو خط رگرسیون در جهت محور Y به سمت بالا یا پایین جابهجایی دارند. در نمودار زیر، میتوان مشاهده نمود که متغیر خروجی تحت شرایط B (روش آزمون B) بالاتر از شرایط A (روش آزمون A) برای هر یک از مقادیر ورودی داده شده است. هدف تعیین آن است که آیا این تغییر مکان عمودی از نظر آماری معنادار است؟

جهت آزمون تفاوت بین ضرایب عرض از مبداء، فقط نیاز به یک متغیر جهت طبقهبندی شرایط مختلف وجود دارد که این متغیر بایستی از نوع وصفی باشد. برای مثالهای استفاده شده در این پست یک متغیر وصفی برای تعیین شرایط (A or B) در هر یک از مشاهدات بکار گرفته شده است.
برازش مدل رگرسیونی در نرم افزار MINITAB از مسیر زیر برای مثال ارائه شده قابل انجام است:
Stat > Regression > Regression > Fit Regression Model
response variable: Output
continuous predicotr: Input
categorical predictor: Condition
در خروجی آنالیز رگرسیون ابتدا جدول ضرایب بررسی میشود:

این جدول نشان می دهد که رابطه بین دو متغیر ورودی (Input) و خروجی (Output) با توجه به آنکه مقدار P-Value برابر با ۰٫۰۰۰ شده است، از نظر آماری معنی دار می باشد.
ضریب عرض از مبداء برای متغیر وصفی شرایط مختلف برابر ۱۰ و مقدار P-Value آن (۰٫۰۰۰) میباشد که نشان میدهد عرض از مبداء در دو معادله رگرسیونی بدست آمده تفاوت معناداری دارند و فرضیه صفر که برابری عرض از مبداءها در دو معادله رگرسیونی است، رد می شود. همچنین می توان تفاوت بین دو ضریب عرض از مبداء را در جدول معادله رگرسیون زیر نیز مشاهده نمود.

3- بررسی تفاوت معنادار آماری در دو معادله رگرسیون
نمودار زیر را در نظر بگیرید، یک مقدار واحد برای متغیر ورودی در دو معادله پاسخ های متفاوتی را ارائه می دهند. به نظر می رسد افزایش یک واحد در متغیر ورودی در وضعیت B افزایش بیشتری را نسبت به وضعیت A دارد. این شرایط در نمودار به صورت بصری مشخص است، بررسی وجود تفاوت آماری معنادار در شیب دو معادله خط مدنظر است.

انجام آزمون آماری تفاوت بین ضرایب شیب خط به نظر مشکل است؛ اما در واقع این امر بسیار ساده و مشابه با مثال قبل قابل انجام میباشد و تنها بایستی تعیین کرد که آیا ضرایب شیب خط وابسته به متغیر وضعیت است. در علم آمار، زمانی می گویند که تاثیر یک متغیر وابسته به متغیر دیگر است، که اثر متقابل (interaction) وجود داشته باشد. لذا آنچه که باید انجام دهیم آن است که تعیین کنیم که آیا اثر متقابل بین دو متغیر Input*Condition وجود دارد یا خیر.
در MINITAB میتوان وجود اثر متقابل را در پنجره تجزیه و تحلیل داده ها رگرسیون بررسی کرد. بعد از آنکه مدل رگرسیون برازش گردید وجود یا عدم وجود اثر متقابل (interaction) به راحتی قابل کنترل است. برای مثال به جدول زیر توجه نمایید.

جدول فوق نشان می دهد اثر متقابل بین دو متغیر (Input*Condition) از نظر آماری معنادار است؛ زیرا مقدار p = 0.000 میباشد. در نتیجه، فرض صفر رد و نتیجه گیری میشود که تفاوت بین ضرایب شیب خط (۱٫۵۳۵۹ و ۲٫۰۰۵۰) در دو معادله رگرسیونی برابر با صفر نمیباشد. همچنین مشاهده میشود تفاوت بین عرض از مبدا دو خط برای این مثال با توجه به آنکه (P = 0.093)است، از نظر آماری معنادار نمیباشد و تنها تفاوت معنادار موجود، تفاوت بین شیب دو خط است.

4- سخن پایانی
روش شرح داده شده در این پست برای مقایسه دو معادله روگرسیونی با نام روش حداقل مربعات معمولی شناخته میشود. در این روش فرض بر این است که خطای مشاهدات عمدتاً در محور y است و خطا مشاهدات در محور x ناچیز و قابل صرف نظر کردن است. اگر این فرض برقرار نباشد، بایستی از روش رگرسیون دمینگ استفاده نمود. تفاوت رگرسیون دمینگ با رگرسیون خطی ساده از این جهت است که خطای مشاهدات در هر دو محور x و y را در نظر میگیرد. این یک روش در مقایسه با رگرسیون خطی ساده کمی پیچیدهتر است. در یک پست آموزشی دیگر به عنوان استفاده از رگرسیون دمینگ برای صحه گذاری روش های آزمونپرداخته شده است. در صورت وجود هر گونه پرسشی در خصوص رسم رگرسیون در آزمایشگاه میتواند سوالات خودتان در قسمت کامنت های این پست قراردهید. سعی خواهد شد تا جای ممکن به سئوالات مطرح شده پاسخ مناسب داده شوند. همچنین در صورت نیاز به برگزاری دوره تصدیق و صحه گذاری روش آزمون با نرمافزار Minitab برای کارکنان آزمایشگاه یا برای دریافت خدمات مشاوره استاندارد ایزو 17025 و مشاوره استاندارد ایزو 15189 میتوانید با ما تماس بگیرید.



دیدگاهتان را بنویسید